Rhombicuboctahedron

Rhombicuboctahedron: I geometri er rhombicuboctahedron , eller liten rhombicuboctahedron , et arkimedisk fast stoff med åtte trekantede og atten firkantede flater. Det er 24 identiske hjørner, med en trekant og tre firkanter som møtes på hver. Polyederet har oktaedrisk symmetri, som terningen og oktaedronen. Dens dual kalles deltoidal icositetrahedron eller trapezoidal icositetrahedron, selv om ansiktene egentlig ikke er sanne trapezoids.
Cuboctahedron: En cuboctahedron er et polyeder med 8 trekantede flater og 6 kvadratflater. En cuboctahedron har 12 identiske hjørner, med 2 trekanter og 2 firkanter som møtes på hver, og 24 identiske kanter, som hver skiller en trekant fra en firkant. Som sådan er det et kvasiregulært polyeder, det vil si et arkimedisk fast stoff som ikke bare er toppunkt-transitive, men også kant-transitive. Det er det eneste radialt likesidet konvekse polyeder.
Cantellated tesseract: I fire-dimensjonal geometri er en kantellert tesseract en konveks uniform 4-polytop, som er en kantellasjon av den vanlige tesseracten.
Utbedret 24-cellers: I geometri er den rektifiserte 24-celle eller rektifiserte icositetrachoron en ensartet 4-dimensjonal polytop, som er avgrenset av 48 celler: 24 terninger og 24 cuboctahedra. Den kan oppnås ved å rette opp 24-cellen og redusere dens oktaedriske celler til terninger og kubokta.
Utbedret 24-cellers: I geometri er den rektifiserte 24-celle eller rektifiserte icositetrachoron en ensartet 4-dimensjonal polytop, som er avgrenset av 48 celler: 24 terninger og 24 cuboctahedra. Den kan oppnås ved å rette opp 24-cellen og redusere dens oktaedriske celler til terninger og kubokta.
Cantellated 5-cellers: I fire-dimensjonal geometri er en kantellert 5-celle en konveks uniform 4-polytop, som er en kantellasjon av den vanlige 5-cellen.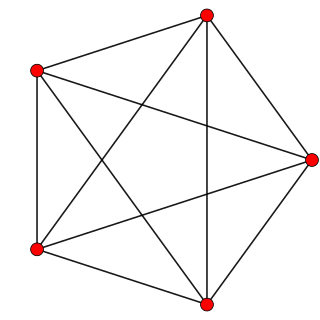
Cantellated 5-cellers: I fire-dimensjonal geometri er en kantellert 5-celle en konveks uniform 4-polytop, som er en kantellasjon av den vanlige 5-cellen.
5-cellers honningkake: I fire-dimensjonal euklidisk geometri er den 4-simplex honningkake , 5-cellers honningkake eller pentakorisk-dispentakorisk honningkake en romfyllende tessellasjonskake. Den består av 5-celler og rektifiserte 5-cellers fasetter i et forhold på 1: 1.
Cantellated 5-terninger: I seksdimensjonal geometri er en kantellert 5-kube en konveks uniform 5-polytop, som er en kantellasjon av den vanlige 5-kuben.
Cantellated 5-terninger: I seksdimensjonal geometri er en kantellert 5-kube en konveks uniform 5-polytop, som er en kantellasjon av den vanlige 5-kuben.
Runcic 5-terninger: I seksdimensjonal geometri er en runkisk 5-kube eller en konveks uniform 5-polytop. Det er 2 runkiske former for 5-terningen. Runcic 5-terninger har halvparten av hjørnene til runcinated 5-terninger.
Runcic 5-terninger: I seksdimensjonal geometri er en runkisk 5-kube eller en konveks uniform 5-polytop. Det er 2 runkiske former for 5-terningen. Runcic 5-terninger har halvparten av hjørnene til runcinated 5-terninger.
Cantellated 5-ortoplexes: I femdimensjonal geometri er en kantellert 5-ortoplex en konveks uniform 5-polytop, som er en kantellasjon av den vanlige 5-ortoplexen.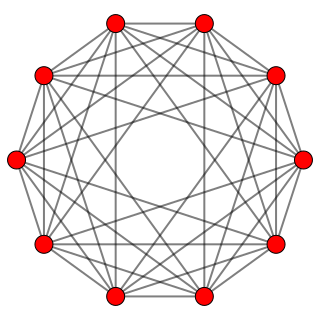
Cantellated 5-ortoplexes: I femdimensjonal geometri er en kantellert 5-ortoplex en konveks uniform 5-polytop, som er en kantellasjon av den vanlige 5-ortoplexen.
Cantellated 5-simplexer: I femdimensjonal geometri er en kantellert 5-simplex en konveks uniform 5-polytop, som er en kantellasjon av den vanlige 5-simplexen.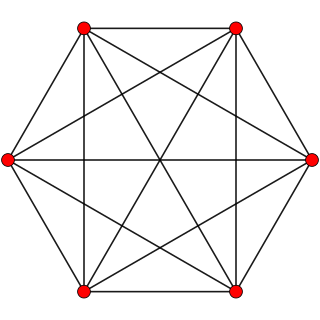
Cantellated 5-simplexer: I femdimensjonal geometri er en kantellert 5-simplex en konveks uniform 5-polytop, som er en kantellasjon av den vanlige 5-simplexen.
Cantellated 6-terninger: I seksdimensjonal geometri er en kantellert 6-kube en konveks ensartet 6-polytop, som er en kantellasjon av den vanlige 6-kuben.
Cantellated 6-terninger: I seksdimensjonal geometri er en kantellert 6-kube en konveks ensartet 6-polytop, som er en kantellasjon av den vanlige 6-kuben.
Runcic 6-terninger: I seksdimensjonal geometri er en runkisk 6-kube en konveks uniform 6-polytop. Det er 2 unike runcic for 6-terningen.
Runcic 6-terninger: I seksdimensjonal geometri er en runkisk 6-kube en konveks uniform 6-polytop. Det er 2 unike runcic for 6-terningen.
Cantellated 6-ortoplexer: I seksdimensjonal geometri er en kantellert 6-ortoplex en konveks uniform 6-polytop, som er en kantellasjon av den vanlige 6-ortoplexen.
Cantellated 6-ortoplexer: I seksdimensjonal geometri er en kantellert 6-ortoplex en konveks uniform 6-polytop, som er en kantellasjon av den vanlige 6-ortoplexen.
Cantellated 6-simplexer: I seksdimensjonal geometri er en kantellert 6-simplex en konveks uniform 6-polytop, som er en kantellasjon av den vanlige 6-simplexen.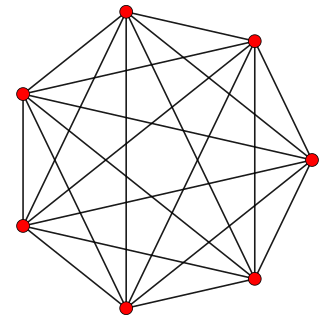
Cantellated 6-simplexer: I seksdimensjonal geometri er en kantellert 6-simplex en konveks uniform 6-polytop, som er en kantellasjon av den vanlige 6-simplexen.
Kantellert 120-celle: I fire-dimensjonal geometri er en kantellert 120-celle en konveks uniform 4-polytop, som er en kantellasjon av den vanlige 120-cellen.
7-terningskanteller: I syvdimensjonal geometri er en kantellert 7-terning en konveks uniform 7-polytop, som er en kantellasjon av den vanlige 7-terningen.
7-terningskanteller: I syvdimensjonal geometri er en kantellert 7-terning en konveks uniform 7-polytop, som er en kantellasjon av den vanlige 7-terningen.
Runcic 7-terninger: I sju-dimensjonal geometri er en runkisk 7-kube en konveks uniform 7-polytop, relatert til den uniforme 7-demicube. Det er 2 unike former.
Runcic 7-terninger: I sju-dimensjonal geometri er en runkisk 7-kube en konveks uniform 7-polytop, relatert til den uniforme 7-demicube. Det er 2 unike former.
Cantellated 7-ortoplexer: I syvdimensjonal geometri er en kantellert 7-ortoplex en konveks uniform 7-polytop, som er en kantellasjon av den vanlige 7-ortoplexen.
Cantellated 7-ortoplexer: I syvdimensjonal geometri er en kantellert 7-ortoplex en konveks uniform 7-polytop, som er en kantellasjon av den vanlige 7-ortoplexen.
Cantellated 7-simplexer: I syvdimensjonal geometri er en kantellert 7-simplex en konveks uniform 7-polytop, som er en kantellasjon av den vanlige 7-simplexen.
Cantellated 7-simplexer: I syvdimensjonal geometri er en kantellert 7-simplex en konveks uniform 7-polytop, som er en kantellasjon av den vanlige 7-simplexen.
Cantellated tesseract: I fire-dimensjonal geometri er en kantellert tesseract en konveks uniform 4-polytop, som er en kantellasjon av den vanlige tesseracten.
Uniform 8-polytop: I åttedimensjonal geometri er en åttedimensjonal polytop eller 8-polytop en polytop som er inneholdt av 7-polytopfasetter. Hver 6-polytoprygge deles av nøyaktig to 7-polytopfasetter.
Cantellated 8-simplexer: I åtte-dimensjonal geometri er en kantellert 8-simplex en konveks uniform 8-polytop, som er en kantellasjon av den vanlige 8-simplexen.
Cantellated 8-simplexer: I åtte-dimensjonal geometri er en kantellert 8-simplex en konveks uniform 8-polytop, som er en kantellasjon av den vanlige 8-simplexen.
Rhombicosidodecahedron: I geometri er rhombicosidodecahedron , et arkimedisk fast stoff, et av tretten konvekse isogonale ikke -prismatiske faste stoffer konstruert av to eller flere typer vanlige polygonflater.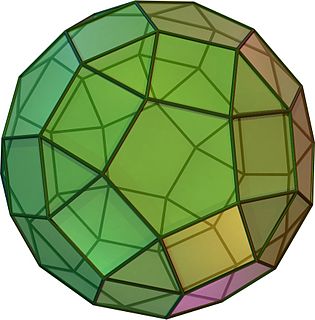
Tetrahedral-oktaedrisk honningkake: Den tetraedrisk-oktaedriske bikaken , vekslet kubisk honningkake er en kvasiregulær romfyllende tessellasjon i euklidisk 3-mellomrom. Den består av alternerende vanlige oktaeder og tetraeder i forholdet 1: 2.
Rhombicuboctahedron: I geometri er rhombicuboctahedron , eller liten rhombicuboctahedron , et arkimedisk fast stoff med åtte trekantede og atten firkantede flater. Det er 24 identiske hjørner, med en trekant og tre firkanter som møtes på hver. Polyederet har oktaedrisk symmetri, som terningen og oktaedronen. Dens dual kalles deltoidal icositetrahedron eller trapezoidal icositetrahedron, selv om ansiktene egentlig ikke er sanne trapezoids.
Kubisk honningkake: Den kubiske honningkaken eller kubikkcelluleringen er den eneste riktige vanlige romfyllende tessellasjonen i euklidisk 3-rom, som består av kubikkceller. Den har 4 terninger rundt hver kant, og 8 kuber rundt hvert toppunkt. Dens toppunkt er en vanlig oktaeder. Det er en selvdobbel tessellasjon med Schläfli-symbolet {4,3,4}. John Horton Conway kaller denne bikaken en cubille .
Kubisk honningkake: Den kubiske honningkaken eller kubikkcelluleringen er den eneste riktige vanlige romfyllende tessellasjonen i euklidisk 3-rom, som består av kubikkceller. Den har 4 terninger rundt hver kant, og 8 kuber rundt hvert toppunkt. Dens toppunkt er en vanlig oktaeder. Det er en selvdobbel tessellasjon med Schläfli-symbolet {4,3,4}. John Horton Conway kaller denne bikaken en cubille .
Uniform 4-polytop: I geometri er en uniform 4-polytop en 4-dimensjonal polytop som er toppunkt-transitiv og hvis celler er ensartede polyeder, og ansikter er vanlige polygoner.
Rhombicosidodecahedron: I geometri er rhombicosidodecahedron , et arkimedisk fast stoff, et av tretten konvekse isogonale ikke -prismatiske faste stoffer konstruert av to eller flere typer vanlige polygonflater.
Sekskantet fliser med honningkake: Innen hyperbolsk geometri er den sekskantede flis-honningkaken en av 11 vanlige parakompakte honningkaker i tredimensjonalt hyperbolsk rom. Det er parakompakt fordi det har celler sammensatt av et uendelig antall ansikter. Hver celle er en sekskantet flis som har hjørner på en horosfære, en overflate i det hyperbolske rommet som nærmer seg et enkelt ideelt punkt i det uendelige.
Cantellated 5-simplexer: I femdimensjonal geometri er en kantellert 5-simplex en konveks uniform 5-polytop, som er en kantellasjon av den vanlige 5-simplexen.
Icosahedral honningkake: Den icosahedral honeycomb er en av fire kompakte vanlige plassfyllende tessellasjoner i hyperbolsk 3-space. Med Schläfli -symbolet {3,5,3} er det tre icosahedra rundt hver kant og 12 icosahedra rundt hvert toppunkt, i en vanlig dodecahedral toppunktfigur.
Rhombicosidodecahedron: I geometri er rhombicosidodecahedron , et arkimedisk fast stoff, et av tretten konvekse isogonale ikke -prismatiske faste stoffer konstruert av to eller flere typer vanlige polygonflater.
Rhombicuboctahedron: I geometri er rhombicuboctahedron , eller liten rhombicuboctahedron , et arkimedisk fast stoff med åtte trekantede og atten firkantede flater. Det er 24 identiske hjørner, med en trekant og tre firkanter som møtes på hver. Polyederet har oktaedrisk symmetri, som terningen og oktaedronen. Dens dual kalles deltoidal icositetrahedron eller trapezoidal icositetrahedron, selv om ansiktene egentlig ikke er sanne trapezoids.
Order-4 dodecahedral honeycomb: I geometrien til det hyperbolske 3-mellomrom er orden-4 dodekaedriske honningkake en av fire kompakte vanlige romfyllende tessellasjoner. Med Schläfli -symbolet {5,3,4} har det fire dodekaeder rundt hver kant, og åtte dodekaeder rundt hvert toppunkt i et oktaedrisk arrangement. Dens hjørner er konstruert av 3 ortogonale akser. Dens doble er ordre-5 kubikk honningkake.
Order-4 sekskantede fliser honningkake: Innen hyperbolsk geometri oppstår orden-4 sekskantet flis-honningkake som en av 11 vanlige parakompakte honningkaker i tredimensjonalt hyperbolsk rom. Det er parakompakt fordi det har celler sammensatt av et uendelig antall ansikter. Hver celle er en sekskantet flis som har hjørner på en horosfære: et flatt plan i hyperbolsk rom som nærmer seg et enkelt ideelt punkt i det uendelige.
Order-4 octahedral honeycomb: Order-4 octahedral honeycomb er en vanlig paracompact honeycomb i hyperbolsk 3-space. Det er parakompakt fordi det har uendelige toppunktfigurer, med alle hjørner som ideelle punkter ved uendelig. Gitt av Schläfli -symbolet {3,4,4}, har den fire ideelle oktaeder rundt hver kant, og uendelig oktaeder rundt hvert toppunkt i en firkantet flisepunkt.
Order-4 square fliser honeycomb: I geometrien til hyperbolsk 3-mellomrom er bestilling-4 firkantet flis-honningkake en av 11 parakompakte vanlige honningkaker. Det er parakompakt fordi det har uendelige celler og toppunktfigurer, med alle hjørner som ideelle punkter ved uendelig. Gitt av Schläfli -symbolet {4,4,4}, har den fire firkantede fliser rundt hver kant og uendelige firkantede fliser rundt hvert toppunkt i en firkantet flisepunkt.
Order-5 cubic honeycomb: Order-5 cubic honeycomb er en av fire kompakte vanlige romfyllende tessellasjoner i hyperbolsk 3-space. Med Schläfli -symbolet {4,3,5} har det fem kuber {4,3} rundt hver kant og 20 kuber rundt hvert toppunkt. Det er dobbelt med ordre-4 dodekaedriske honningkake.
Order-5 dodecahedral honeycomb: Order-5 dodecahedral honeycomb er en av fire kompakte vanlige romfyllende tessellasjoner i hyperbolsk 3-space. Med Schläfli -symbolet {5,3,5} har den fem dodecahedral -celler rundt hver kant, og hvert toppunkt er omgitt av tjue dodecahedra. Dens toppunkt er en icosahedron.
Order-5 sekskantede fliser honningkake: Innen hyperbolsk geometri oppstår orden-5 sekskantet flis-honningkake som en av 11 vanlige parakompakte honningkaker i tredimensjonalt hyperbolsk rom. Det er parakompakt fordi det har celler sammensatt av et uendelig antall ansikter. Hver celle består av en sekskantet flislegging hvis hjørner ligger på en horosfære, et flatt plan i hyperbolsk rom som nærmer seg et enkelt ideelt punkt i det uendelige.
Order-5 sekskantede fliser honningkake: Innen hyperbolsk geometri oppstår orden-5 sekskantet flis-honningkake som en av 11 vanlige parakompakte honningkaker i tredimensjonalt hyperbolsk rom. Det er parakompakt fordi det har celler sammensatt av et uendelig antall ansikter. Hver celle består av en sekskantet flislegging hvis hjørner ligger på en horosfære, et flatt plan i hyperbolsk rom som nærmer seg et enkelt ideelt punkt i det uendelige.
Order-6 cubic honeycomb: Order-6 cubic honeycomb er en parakompakt vanlig romfyllende tessellasjon i hyperbolsk 3-space. Det er parakompakt fordi det har toppunktfigurer sammensatt av et uendelig antall fasetter, med alle hjørner som ideelle punkter ved uendelig. Med Schläfli -symbolet {4,3,6} har bikaken seks ideelle terninger som møtes langs hver kant. Dens toppunkt er en uendelig trekantet flislegging. Dens doble er ordre-4 sekskantede fliser honningkake.
Order-6 dodecahedral honeycomb: Order-6 dodecahedral honeycomb er en av 11 parakompakte vanlige honeycombs i hyperbolsk 3-space. Det er parakompakt fordi det har toppunktfigurer sammensatt av et uendelig antall ansikter, med alle hjørner som ideelle punkter ved uendelig. Den har Schläfli -symbolet {5,3,6}, med seks ideelle dodecahedral -celler som omgir hver kant av bikaken. Hvert toppunkt er ideelt, og omgitt av uendelig mange dodekaeder. Honeycomb har en trekantet fliser toppunkt figur.
Order-6 sekskantede fliser honningkake: Innen hyperbolsk geometri er ordre-6 sekskantet flis-honningkake en av 11 vanlige parakompakte honningkaker i tredimensjonalt hyperbolsk rom. Det er parakompakt fordi det har celler med et uendelig antall ansikter. Hver celle er en sekskantet flis som har hjørner på en horosfære: et flatt plan i hyperbolsk rom som nærmer seg et enkelt ideelt punkt i det uendelige.
Order-6 tetrahedral honningkake: I hyperbolsk 3-rom er order-6 tetrahedral honningkake en parakompakt vanlig romfyllende tessellasjon. Det er parakompakt fordi det har toppunktfigurer sammensatt av et uendelig antall ansikter, og har alle hjørner som ideelle punkter ved uendelig. Med Schläfli-symbolet {3,3,6} har order-6 tetrahedral honningkake seks ideelle tetraeder rundt hver kant. Alle hjørner er ideelle, med uendelig mange tetraeder som eksisterer rundt hvert toppunkt i en trekantet flisepunkt.
Cantellated 5-cellers: I fire-dimensjonal geometri er en kantellert 5-celle en konveks uniform 4-polytop, som er en kantellasjon av den vanlige 5-cellen.
Kantellasjon (geometri): I geometri er en kantellasjon en 2. orden avkortning i en hvilken som helst dimensjon som avfaser en vanlig polytop ved kantene og i hjørnene, og skaper en ny fasett i stedet for hver kant og for hvert toppunkt. Cantellation gjelder også vanlige fliser og honningkaker. Cantellating er også å rette opp dens utbedring.
Firkantet fliser honningkake: I geometrien til hyperbolsk 3-mellomrom er den firkantede flisbelegget en av 11 parakompakte vanlige honningkaker. Det kalles parakompakt fordi det har uendelige celler, hvis hjørner eksisterer på horosfærer og konvergerer til et enkelt ideelt punkt i det uendelige. Gitt av Schläfli -symbolet {4,4,3}, har den tre firkantede fliser, {4,4}, rundt hver kant og seks firkantede fliser rundt hvert toppunkt i en kubisk {4,3} toppunkt.
Cantellated tesseract: I fire-dimensjonal geometri er en kantellert tesseract en konveks uniform 4-polytop, som er en kantellasjon av den vanlige tesseracten.
Cantellated tesseractic honeycomb: I den fire-dimensjonale euklidiske geometrien er den kantellerte tesseraktiske honningkaken en ensartet romfyllende tessellasjon i euklidisk 4-mellomrom. Den er konstruert av en kantellasjon av en tesseraktisk honningkake som skaper kantellerte tesserakter og nye 24-cellers og oktaedriske prisme-fasetter ved de opprinnelige hjørnene.
Cuboctahedral prisme: I geometri er et cuboctahedral prisme en konveks uniform 4-polytop. Denne 4-polytopen har 16 polyhedrale celler: 2 kuboctahedra forbundet med 8 trekantede prismer og 6 terninger.
Cuboctahedron: En cuboctahedron er et polyeder med 8 trekantede flater og 6 kvadratflater. En cuboctahedron har 12 identiske hjørner, med 2 trekanter og 2 firkanter som møtes på hver, og 24 identiske kanter, som hver skiller en trekant fra en firkant. Som sådan er det et kvasiregulært polyeder, det vil si et arkimedisk fast stoff som ikke bare er toppunkt-transitive, men også kant-transitive. Det er det eneste radialt likesidet konvekse polyeder.
Trekantet fliser honningkake: Den trekantede flisbelegget er en av 11 parakompakte vanlige romfyllende tessellasjoner i hyperbolsk 3-mellomrom. Det kalles parakompakt fordi det har uendelige celler og toppunktfigurer, med alle hjørner som ideelle punkter ved uendelig. Den har Schläfli -symbolet {3,6,3}, og består av trekantede fliser. Hver kant av bikaken er omgitt av tre celler, og hvert toppunkt er ideelt med uendelig mange celler som møtes der. Dens toppunkt er en sekskantet flis.
Kantellasjon (geometri): I geometri er en kantellasjon en 2. orden avkortning i en hvilken som helst dimensjon som avfaser en vanlig polytop ved kantene og i hjørnene, og skaper en ny fasett i stedet for hver kant og for hvert toppunkt. Cantellation gjelder også vanlige fliser og honningkaker. Cantellating er også å rette opp dens utbedring.
Kantellasjon (geometri): I geometri er en kantellasjon en 2. orden avkortning i en hvilken som helst dimensjon som avfaser en vanlig polytop ved kantene og i hjørnene, og skaper en ny fasett i stedet for hver kant og for hvert toppunkt. Cantellation gjelder også vanlige fliser og honningkaker. Cantellating er også å rette opp dens utbedring.
Cantelli: Cantelli er et italiensk etternavn. Kjente personer med etternavnet inkluderer: Claudio Cantelli, brasiliansk racerfører Francesco Paolo Cantelli (1875–1966), italiensk matematiker Guido Cantelli (1920–1956), italiensk dirigent Ugo Cantelli (1903–1972), italiensk sportsskytter
Cantellis ulikhet: I sannsynlighetsteorien er Cantellis ulikhet en generalisering av Tsjebysjevs ulikhet når det gjelder en enkelt "hale". Ulikheten sier at
Cantelli Awards: Cantelli -prisen anerkjenner dyktighet i å dirigere. Prisen ble først delt ut 3. oktober 1961. Prisene ble arrangert på Teatro Coccia, i Novara, der også alle de andre utgavene ble arrangert. Den prestisjetunge prisen ble blant annet vunnet av Ádám Fischer, Lothar Zagrosek og Riccardo Muti, som var den første italieneren som vant prisen. Mange vinnere av prisen ble fremtredende dirigenter.
Francesco Paolo Cantelli: Francesco Paolo Cantelli var en italiensk matematiker.
Cantellis ulikhet: I sannsynlighetsteorien er Cantellis ulikhet en generalisering av Tsjebysjevs ulikhet når det gjelder en enkelt "hale". Ulikheten sier at
Cantello: Cantello er en kommune (kommune) i provinsen Varese i den italienske regionen Lombardia, som ligger omtrent 45 kilometer nordvest for Milano og omtrent 4 kilometer øst for Varese, på grensen til Sveits. Desember 2004 hadde den en befolkning på 4 409 og et område på 9,1 kvadratkilometer.
Cantello (disambiguation): Cantello er en italiensk kommune.
Andrea Cantelmo: Andrea Cantelmo var en napolitansk kommandør for Habsburg-hærene under tretti års krig, krigen om den mantuanske arvefølgen, den andre fasen av åttiårskrigen og den fransk-spanske krigen (1635–59).
Cantelmo slott: Castello Cantelmo er et middelalderslott i Pettorano sul Gizio, provinsen L'Aquila, Abruzzo, Sør-Sentral-Italia.
Cantelo: Cantelo var en britisk fullblodshest og avlshopp. I en karriere som varte fra våren 1958 til september 1959 løp hun elleve ganger og vant åtte løp. Cantelo var ubeseiret i fem løp som toåring inkludert Royal Lodge Stakes, der hun beseiret hingst. Som treåring i 1959 vant hun Classic St Leger, i tillegg til Cheshire Oaks og Ribblesdale Stakes. Nederlagene hennes kom da hun endte på andreplass i The Oaks og Park Hill Stakes og løp fjerde til Alcide i King George VI og Queen Elizabeth Stakes. Hun ble pensjonist fra racing etter seieren i St Leger og hadde en viss suksess som stamme.
William Cantelo: William Cantelo var en britisk oppfinner fra 1800-tallet. Kreditt for å utvikle et tidlig maskingevær, forsvant han fra hjemmet i Southampton på 1880 -tallet. Mens han prøvde å finne Cantelo, så hans to sønner et fotografi av amerikanskfødte oppfinner Hiram Maxim, skaperen av Maxim-pistolen; hans overfladiske likhet med faren fikk dem til å tro at han hadde dukket opp igjen under et nytt navn.
Cantelon: Cantelon er et etternavn. Kjente personer med etternavnet inkluderer: Ben Cantelon, kanadisk musiker Paul Cantelon, amerikansk komponist Philip L. Cantelon, amerikansk forretningsmann Reg Cantelon (1902–1993), kanadisk politiker Ron Cantelon, kanadisk politiker
Paul Cantelon: Paul Cantelon er en amerikansk samtidsklassisk musikk og populærmusikk, en komponist og en skuespiller.
Cantaloupe: Cantaloupe, rockmelon, søt melon, eller spanspek er en melon som er et utvalg av de muskmelon arter fra familien Cucurbitaceae.
Cantaloupe Island: "Cantaloupe Island" er en jazzstandard komponert av Herbie Hancock og spilt inn for albumet Empyrean Isles fra 1964 i de første årene som et av medlemmene i Miles Davis 'kvintett fra 1960 -tallet.
Joseph Canteloube: Marie-Joseph Canteloube de Malaret var en fransk komponist, musikkolog og forfatter mest kjent for sine samlinger av orkestrerte folkesanger fra Auvergne-regionen, Chants d'Auvergne .
Joseph Canteloube: Marie-Joseph Canteloube de Malaret var en fransk komponist, musikkolog og forfatter mest kjent for sine samlinger av orkestrerte folkesanger fra Auvergne-regionen, Chants d'Auvergne .
Canteloup: Canteloup kan referere til kommuner i Frankrike: Canteloup, Calvados, i departementet Calvados Canteloup, Manche, i departementet Manche
Canteloup, Calvados: Canteloup er en kommune i Calvados -avdelingen i Normandie -regionen i Nordvest -Frankrike.
Canteloup, Manche: Canteloup er en kommune i Manche-avdelingen i Normandie i det nordvestlige Frankrike.
Cantaloupe: Cantaloupe, rockmelon, søt melon, eller spanspek er en melon som er et utvalg av de muskmelon arter fra familien Cucurbitaceae.
Cantaloupe: Cantaloupe, rockmelon, søt melon, eller spanspek er en melon som er et utvalg av de muskmelon arter fra familien Cucurbitaceae.
Lewisia cantelovii: Lewisia cantelovii er en uvanlig art av blomstrende plante i familien Montiaceae kjent under det vanlige navnet Cantelow's lewisia . Det er endemisk til California, hvor det er kjent fra de nordøstlige fjellkjedene fra Klamath -fjellene til det nordlige Sierra Nevada. Den vokser i steinete, fuktige fjellhabitater. Dette er en flerårig urt som vokser fra en kort, tykk taprot- og caudex -enhet. Den produserer en basal rosett av tykke, kjøttfulle, skjeformede skjeformede blader med takkete kanter. Blomsterstanden er en veldig slank oppreist stamme opp til 45 centimeter høy toppet med en spredt bunn av blomster og kjertelformede, tannede bladblad. Hver blomst har 5 til 7 ovale kronblad hver halv til en centimeter lang. Kronbladene er hvite eller veldig blekrosa med skarpe mørkrosa vener. I midten av blomsten er fem støvdragere tippet med mørkrosa støvknapper.
Cantelowes (avdeling): Cantelowes er en avdeling i London Borough of Camden, i Storbritannia. Avdelingen har eksistert siden lokalvalget i mai 2002 og dekker et område mellom Kentish Town Road og York Way.
Cantelowes (avdeling): Cantelowes er en avdeling i London Borough of Camden, i Storbritannia. Avdelingen har eksistert siden lokalvalget i mai 2002 og dekker et område mellom Kentish Town Road og York Way.
Cantaloupe (disambiguation): Cantaloupe er en frukt.
Château Cantemerle: Château Cantemerle er en vingård i Haut-Médoc-appellasjonen i vinregionen Bordeaux i Frankrike, i kommunen Macau. Vinen som ble produsert her var den endelige eiendommen som ble klassifisert som en av atten Cinquièmes Crus i Bordeaux Wine Official Classification fra 1855. Dens fravær fra klassifiseringskartet på 1855 Exposition Universelle de Paris skapte noen kontroverser, selv om den har blitt listet opp på alle kart publisert etter 1855. Noen kilder vil inkludere en stjerne ved siden av Château Cantemerle -oppføringen med henvisning til denne kontroversen. Godset har en lang historie i Haut-Médoc med poster som beskriver dens eksistens siden minst 1100-tallet og vinproduksjon siden minst 1300-tallet. På 1800 -tallet ble eiendommen hardt rammet av phylloxera -epidemien, samt angrep av vinstokker av dunete mugg, hvoretter produksjonen falt nesten 50%. Mot slutten av 1900 -tallet ble eiendommen solgt til det franske forsikringskonsernet Les Mutuelles d'Assurance du Bâtiment et des Travaux Public som har bidratt med betydelige investeringer i eiendommens vingårder og vinfremstillingsanlegg.
Cantemir: Cantemir eller Kantemir kan referere til:
Dimitrie Cantemir: Dimitrie eller Demetrius Cantemir , også kjent med andre skrivemåter, var en moldavisk soldat, statsmann og bokstavmann. Han tjente to ganger som voivode i Moldavia. I løpet av sin andre periode allierte han sin stat med Russland i en krig mot Moldavias osmanske overherrer; Russlands nederlag tvang Cantemirs familie i eksil og erstatningen av de opprinnelige voivodene med greske phanarioter. Cantemir var også en produktiv skribent, forskjellige filosofer, historikere, komponister, musikkvitere, lingvister, etnografer og geografer. Sønnen Antiokia, Russlands ambassadør i Storbritannia og Frankrike og en venn av Montesquieu og Voltaire, ville bli kjent som "faren til russisk poesi".
Maria Cantemir: Maria Cantemir var en rumensk adelskvinne, prinsesse av Moldavia, en dame i ventetid og frisørsalong, og en elskerinne av Peter den store, keiseren i Russland.
Cantemir, Moldova: Cantemir er en by i Moldova. Det er det administrative sentrum i Cantemir -distriktet.
Cantemir, Oradea: Cantemir er et distrikt i den rumenske byen Oradea.
Cantemir: Cantemir eller Kantemir kan referere til:
Cantemir -distriktet: Cantemir er et distrikt sør i Moldova, med det administrative senteret i Cantemir. Fra 1. januar 2011 var befolkningen 62 800.
Cantemir -distriktet: Cantemir er et distrikt sør i Moldova, med det administrative senteret i Cantemir. Fra 1. januar 2011 var befolkningen 62 800.
Cantemir -distriktet: Cantemir er et distrikt sør i Moldova, med det administrative senteret i Cantemir. Fra 1. januar 2011 var befolkningen 62 800.
Cantemirești: Cantemirești eller Cantemir var en moldavisk boyarfamilie. Familien var av tatarisk opprinnelse, og kom fra Krim på 1600 -tallet. På 1600- og 1700 -tallet kom det frem flere Voivodes i Moldavia. På 1700 -tallet flyttet familien til Russland, Storbritannia og Frankrike.
Cantemir -palasset i Istanbul: Palace of Dimitrie Cantemir var et palass som eies av prinsen av Moldavia Dimitrie Cantemir i Istanbul, som ligger på den nåværende Ortaköy-moskeen.
Cantemir Vodă National College: Cantemir Vodă National College er en videregående skole i Bucuresti, Romania. Det ble grunnlagt 27. oktober 1868.
Cantemir Vodă National College: Cantemir Vodă National College er en videregående skole i Bucuresti, Romania. Det ble grunnlagt 27. oktober 1868.
Cantemir -distriktet: Cantemir er et distrikt sør i Moldova, med det administrative senteret i Cantemir. Fra 1. januar 2011 var befolkningen 62 800.
Cantemirești: Cantemirești eller Cantemir var en moldavisk boyarfamilie. Familien var av tatarisk opprinnelse, og kom fra Krim på 1600 -tallet. På 1600- og 1700 -tallet kom det frem flere Voivodes i Moldavia. På 1700 -tallet flyttet familien til Russland, Storbritannia og Frankrike.
Nedre Donau storbyområde: Donau storbyområde eller Galați-Brăila storbyområde er et foreslått byområdeprosjekt i Romania. Det ville bli dannet fra byene Galați og Brăila. Til sammen har de en befolkning på rundt 430 000 mennesker.
Cantemirești: Cantemirești eller Cantemir var en moldavisk boyarfamilie. Familien var av tatarisk opprinnelse, og kom fra Krim på 1600 -tallet. På 1600- og 1700 -tallet kom det frem flere Voivodes i Moldavia. På 1700 -tallet flyttet familien til Russland, Storbritannia og Frankrike.
Cantemirești: Cantemirești eller Cantemir var en moldavisk boyarfamilie. Familien var av tatarisk opprinnelse, og kom fra Krim på 1600 -tallet. På 1600- og 1700 -tallet kom det frem flere Voivodes i Moldavia. På 1700 -tallet flyttet familien til Russland, Storbritannia og Frankrike.
Cantemirești: Cantemirești eller Cantemir var en moldavisk boyarfamilie. Familien var av tatarisk opprinnelse, og kom fra Krim på 1600 -tallet. På 1600- og 1700 -tallet kom det frem flere Voivodes i Moldavia. På 1700 -tallet flyttet familien til Russland, Storbritannia og Frankrike.
Cantemus: Cantemus er et litauisk kammerkor. Det ble grunnlagt i 1986 i Vilnius, Litauen. Den første konserten ble holdt samme år 31. desember i St. Casimir's Church. På kort tid ble koret vinner av mange konkurranser og ble tildelt tittelen "Eksemplarisk kor".
Cantemus: Cantemus er et litauisk kammerkor. Det ble grunnlagt i 1986 i Vilnius, Litauen. Den første konserten ble holdt samme år 31. desember i St. Casimir's Church. På kort tid ble koret vinner av mange konkurranser og ble tildelt tittelen "Eksemplarisk kor".
Sangen om Moses: Moses sang er navnet noen ganger gitt til diktet som vises i 5. Mosebok 32: 1–43 i den hebraiske bibelen, som ifølge Bibelen ble levert like før Moses døde på Nebo -fjellet. Noen ganger omtales sangen som 5. Mosebok 32 , til tross for at 5. Mosebok kapittel 32 strengt tatt inneholder ni vers (44–52) som ikke er en del av sangen.
Cantenac: Cantenac er en tidligere kommune i Gironde-avdelingen i Nouvelle-Aquitaine i det sørvestlige Frankrike. Januar 2017 ble det slått sammen til den nye kommunen Margaux-Cantenac. Det ligger i nærheten av Bordeaux.