Cantina Tollo

Cantina Tollo: Cantina Tollo var et italiensk sykkellag aktivt fra 1996 til 2002.
Cantina Tollo: Cantina Tollo var et italiensk sykkellag aktivt fra 1996 til 2002.
Kantiner: Cantiñas er en gruppe flamenco palos , som har sin opprinnelse i området Cádiz i Andalucía. De deler samme kompás eller rytmiske mønster med soleá og blir vanligvis sunget i en livlig rytme. De blir vanligvis sunget i major -modus og har en festlig stemning.
Cantine: Cantine er et etternavn. Kjente personer med etternavnet inkluderer: David Cantine, kanadisk maler John Cantine (1735–1808), amerikansk politiker Moses I. Cantine (1774–1823), amerikansk politiker, dommer og avisredaktør
David Cantine: David Cantine er en kanadisk maler, mest kjent for å ha konsekvent malt bilder med samme komposisjon de siste førti årene av karrieren.Cantine ble født i Jackson, Michigan, og gikk på skole ved University of Iowa og tjente en Bachelor of Arts -grad i 1962, og en Master of Arts -grad i 1964. I 1965 begynte han å undervise i tegning og maleri ved University of Alberta, til han trakk seg fra stillingen i 1996.
James Cantine: Pastor James Cantine , DD var en amerikansk misjonær, lærd og reisende. Mens han studerte ved New Brunswick Theological Seminary i New Jersey, grunnla han Arabian Mission med John Lansing og Samuel Marinus Zwemer. Oppdraget eksisterer i dag som American Mission Hospital i Bahrain. Han var misjonær i førti år, som inkluderte etablering av det første oppdraget for den reformerte kirken i Arabia, som også var det første oppdraget i Øst -Arabia. Mellom 1891 og 1929 etablerte han misjonsposter, medisinske klinikker og kirker i Arabia.
John Cantine: John Cantine var en amerikansk politiker.
Ferrari Trento: Ferrari F.lli Lunelli SpA, eller Ferrari Trento eller Cantine Ferrari, er et italiensk selskap som spesialiserer seg på produksjon av musserende tradisjonell metode, også kalt Metodo Classico eller Méthode Classique. Ferrari Trento er det største selskapet i Lunelli Group, et selskap med seks forskjellige merker som driver vin, flaskevann (Surgiva), grappa og brennevin (Segnana). Lunelli Group har også en to-stjerners Michelin-restaurant, Locanda Margon.
Cantine Lungarotti vingård: Cantine Giorgio Lungarotti Winery srl er et italiensk vinfirma som ligger i regionen Umbria, Italia. Eiendommen er delt mellom flere steder, med den største i byene Torgiano og Montefalco. Selskapet ble grunnlagt på slutten av 1950 -tallet av Giorgio Lungarotti, og ledes nå av kona Maria Grazia og søstrene Teresa og Chiara. Lungarotti -navnet er kjent for å sette umbriske viner på kartet, gjennom en blanding av tradisjonell respekt for landet og moderne innovasjon og forskning. Lungarotti -selskapet eier også Wine Museum of Torgiano (MUVIT) og Olive and Oil Museum (MOO), alle to som ligger i sentrum av Torgiano.
Cantine Lungarotti vingård: Cantine Giorgio Lungarotti Winery srl er et italiensk vinfirma som ligger i regionen Umbria, Italia. Eiendommen er delt mellom flere steder, med den største i byene Torgiano og Montefalco. Selskapet ble grunnlagt på slutten av 1950 -tallet av Giorgio Lungarotti, og ledes nå av kona Maria Grazia og søstrene Teresa og Chiara. Lungarotti -navnet er kjent for å sette umbriske viner på kartet, gjennom en blanding av tradisjonell respekt for landet og moderne innovasjon og forskning. Lungarotti -selskapet eier også Wine Museum of Torgiano (MUVIT) og Olive and Oil Museum (MOO), alle to som ligger i sentrum av Torgiano.
Pallacanestro Reggiana: Pallacanestro Reggiana , også kjent av sponsorhensyn som UnaHotels Reggio Emilia , er et italiensk profesjonelt basketballag med base i Reggio Emilia, Emilia-Romagna. Den spiller i LBA fra og med sesongen 2020–21.
Caprino, Sveits: Caprino er en landsby på den sørlige bredden av innsjøen Lugano i den sveitsiske kantonen Ticino, øst for den italienske eksklaven Campione d'Italia og under toppen av Sighignola. Noen 0,5 kilometer øst for landsbyen Caprino ligger Cantine di Caprino , en mindre bosetning. Begge deler politisk sett en del av Castagnola-Cassarate-kvarteret i byen Lugano, selv om Castagnola-Cassarate frem til 1972 var en uavhengig kommune under navnet Castagnola.
Cantinero: Chris Hicken er en britisk sanger, låtskriver og produsent som spiller inn under navnet Cantinero . For tiden basert i Inwood, Manhattan New York, skriver Hicken nøye observert, nøye utformet pop som blander akustiske og spanske gitarer, piano og strykere, med subtile elektroniske teksturer. Debutalbumet, Championship Boxing , ble gitt ut av indiemerket Artemis Records i 2004. Det neste albumet Better for the Metaphor , som ble utgitt i november 2008 på Tinkle Tone Recordings, har blitt oppført som en av de beste CD -ene i 2008 av NPR.
Cantinflas: Mario Fortino Alfonso Moreno Reyes , kjent under artistnavnet Cantinflas , var en meksikansk komiker, skuespiller og filmskaper. Han regnes for å ha vært den mest gjennomførte meksikanske komikeren og feires i hele Latin-Amerika og i Spania som et populært ikon. Humoren hans, lastet med meksikanske språklige trekk ved intonasjon, ordforråd og syntaks, er elsket i alle de spansktalende landene i Latin-Amerika og i Spania og har gitt opphav til en rekke uttrykk, inkludert cantinflear , cantinflada , cantinflesco og cantinflero .
Cantinflas (film): Cantinflas er en meksikansk biografisk komediedramafilm fra 2014 regissert av Sebastián del Amo. Basert på livet til skuespilleren og komikeren Cantinflas, spiller filmen Óscar Jaenada som tittelfiguren, Michael Imperioli, Ilse Salas, Bárbara Mori, Ana Layevska og Adal Ramones. Den hadde premiere 18. september 2014 i Mexico. I USA ble den utgitt 29. august 2014. Den ble valgt som den meksikanske oppføringen for beste fremmedspråklige film ved 87. Academy Awards, men ble ikke nominert.
Cantinflas (film): Cantinflas er en meksikansk biografisk komediedramafilm fra 2014 regissert av Sebastián del Amo. Basert på livet til skuespilleren og komikeren Cantinflas, spiller filmen Óscar Jaenada som tittelfiguren, Michael Imperioli, Ilse Salas, Bárbara Mori, Ana Layevska og Adal Ramones. Den hadde premiere 18. september 2014 i Mexico. I USA ble den utgitt 29. august 2014. Den ble valgt som den meksikanske oppføringen for beste fremmedspråklige film ved 87. Academy Awards, men ble ikke nominert.
Cantinflas Show: Cantinflas Show er en meksikansk animert TV -serie produsert av Televisa. Serien ble laget av Mario Moreno 'Cantinflas' og animert av den spanske animatoren José Luis Moro, som animerte pilotepisoden i 1972.
Amigo og venner: Amigo and Friends er en pedagogisk barneserie som ble basert på den meksikanske tegneserien Cantinflas Show i 1979. Showet, som konsentrerer seg om et bredt spekter av emner som er ment å utdanne barn, følger Amigo, en liten komisk karakter fra Mexico, som fortsetter utdanningsopplevelser gjennom tid og rom og får besøke Shakespeare, se de gamle pyramidene og til og med reise til andre planeter. Den animerte Amigo er basert på den legendariske karakteren Cantinflas spilt av den meksikanske skuespilleren og komikeren Mario Moreno Reyes.
Cantinflas: Mario Fortino Alfonso Moreno Reyes , kjent under artistnavnet Cantinflas , var en meksikansk komiker, skuespiller og filmskaper. Han regnes for å ha vært den mest gjennomførte meksikanske komikeren og feires i hele Latin-Amerika og i Spania som et populært ikon. Humoren hans, lastet med meksikanske språklige trekk ved intonasjon, ordforråd og syntaks, er elsket i alle de spansktalende landene i Latin-Amerika og i Spania og har gitt opphav til en rekke uttrykk, inkludert cantinflear , cantinflada , cantinflesco og cantinflero .
Cantinflas: Mario Fortino Alfonso Moreno Reyes , kjent under artistnavnet Cantinflas , var en meksikansk komiker, skuespiller og filmskaper. Han regnes for å ha vært den mest gjennomførte meksikanske komikeren og feires i hele Latin-Amerika og i Spania som et populært ikon. Humoren hans, lastet med meksikanske språklige trekk ved intonasjon, ordforråd og syntaks, er elsket i alle de spansktalende landene i Latin-Amerika og i Spania og har gitt opphav til en rekke uttrykk, inkludert cantinflear , cantinflada , cantinflesco og cantinflero .
Canting: Tjanting er et pennlignende verktøy som brukes til å påføre flytende varm voks i batikprosessen i Indonesia, nærmere bestemt batik tulis . Tradisjonell Tjanting består av kobbervoksbeholder med liten pipetut og bambushåndtak . Tradisjonell tjanting er laget av kobber, bronse, sink eller jern, men moderne versjon kan bruke teflon.
Kantende armer: Kantende armer er heraldiske lagre som representerer bærerens navn i en visuell ordspill eller rebus.
Liste over Discworld -karakterer: Denne artikkelen inneholder korte biografier for karakterer fra Terry Pratchetts Discworld -serie. Denne listen består av menneskelige karakterer. For biografier om kjente medlemmer av Discworlds "etniske minoriteter", se artiklene for disse rasene. Noen karakterbiografier er også oppført i artikler om organisasjonene de tilhører. For ytterligere biografier om Discworld -karakterer, se tabellen nedenfor.
Kantende armer: Kantende armer er heraldiske lagre som representerer bærerens navn i en visuell ordspill eller rebus.
Canting kjøl: En skrånende kjøl er en form for seilballast, suspendert fra en stiv skråstiver under båten, som kan svinges til en båt under seil for å motvirke seilets krengekraft. Kantkølen må kunne svinge til enten babord eller styrbord, avhengig av gjeldende tak.
Canting kjøl: En skrånende kjøl er en form for seilballast, suspendert fra en stiv skråstiver under båten, som kan svinges til en båt under seil for å motvirke seilets krengekraft. Kantkølen må kunne svinge til enten babord eller styrbord, avhengig av gjeldende tak.
Canting kjøl: En skrånende kjøl er en form for seilballast, suspendert fra en stiv skråstiver under båten, som kan svinges til en båt under seil for å motvirke seilets krengekraft. Kantkølen må kunne svinge til enten babord eller styrbord, avhengig av gjeldende tak.
Matra-Cantinieau MC-101: Matra-Cantinieau MC-101 var et fransk eksperimentelt to-seters helikopter fra begynnelsen av 1950-tallet av konvensjonell halerotorkonfigurasjon, men med motoren montert nær hovedrotoren, over setene.
Vivandière: Vivandière eller cantinière er et fransk navn for kvinner knyttet til militære regimenter som sutlere eller kantinevogtere . Deres faktiske historiske funksjon med å selge vin til troppene og jobbe i kantiner førte til vedtakelsen av navnet 'cantinière' som kom til å erstatte den opprinnelige 'vivandière' fra 1793, men bruken av begge begrepene var vanlig på fransk til midten -1900-tallet, og 'vivandière' forble den valgfrie termen i ikke-fransktalende land som USA, Spania, Italia og Storbritannia. Vivandières tjenestegjorde i den franske hæren fram til begynnelsen av første verdenskrig, men skikken spredte seg til mange andre hærer. Vivandières tjenestegjorde også på begge sider i den amerikanske borgerkrigen, og i hærene i Spania, Italia, de tyske statene, Sveits og forskjellige hærer i Sør -Amerika, selv om lite er kjent om detaljene i de fleste av disse tilfellene, ettersom historikere ikke har gjort omfattende undersøkelser på dem.
Vivandière: Vivandière eller cantinière er et fransk navn for kvinner knyttet til militære regimenter som sutlere eller kantinevogtere . Deres faktiske historiske funksjon med å selge vin til troppene og jobbe i kantiner førte til vedtakelsen av navnet 'cantinière' som kom til å erstatte den opprinnelige 'vivandière' fra 1793, men bruken av begge begrepene var vanlig på fransk til midten -1900-tallet, og 'vivandière' forble den valgfrie termen i ikke-fransktalende land som USA, Spania, Italia og Storbritannia. Vivandières tjenestegjorde i den franske hæren fram til begynnelsen av første verdenskrig, men skikken spredte seg til mange andre hærer. Vivandières tjenestegjorde også på begge sider i den amerikanske borgerkrigen, og i hærene i Spania, Italia, de tyske statene, Sveits og forskjellige hærer i Sør -Amerika, selv om lite er kjent om detaljene i de fleste av disse tilfellene, ettersom historikere ikke har gjort omfattende undersøkelser på dem.
Cantino planisphere: Cantino planisphere eller Cantino verdenskart er et manuskript portugisisk verdenskart bevart på Biblioteca Estense i Modena, Italia. Den er oppkalt etter Alberto Cantino , en agent for hertugen av Ferrara, som med suksess smuglet den fra Portugal til Italia i 1502. Den måler 220 x 105 cm.
Cantino planisphere: Cantino planisphere eller Cantino verdenskart er et manuskript portugisisk verdenskart bevart på Biblioteca Estense i Modena, Italia. Den er oppkalt etter Alberto Cantino , en agent for hertugen av Ferrara, som med suksess smuglet den fra Portugal til Italia i 1502. Den måler 220 x 105 cm.
Cantino planisphere: Cantino planisphere eller Cantino verdenskart er et manuskript portugisisk verdenskart bevart på Biblioteca Estense i Modena, Italia. Den er oppkalt etter Alberto Cantino , en agent for hertugen av Ferrara, som med suksess smuglet den fra Portugal til Italia i 1502. Den måler 220 x 105 cm.
Cantino planisphere: Cantino planisphere eller Cantino verdenskart er et manuskript portugisisk verdenskart bevart på Biblioteca Estense i Modena, Italia. Den er oppkalt etter Alberto Cantino , en agent for hertugen av Ferrara, som med suksess smuglet den fra Portugal til Italia i 1502. Den måler 220 x 105 cm.
Cantino planisphere: Cantino planisphere eller Cantino verdenskart er et manuskript portugisisk verdenskart bevart på Biblioteca Estense i Modena, Italia. Den er oppkalt etter Alberto Cantino , en agent for hertugen av Ferrara, som med suksess smuglet den fra Portugal til Italia i 1502. Den måler 220 x 105 cm.
Cantinoa: Cantinoa er en slekt av planter med 27 arter i familien Lamiaceae, først beskrevet i 2012. Den er hovedsakelig hjemmehørende i New World, med noen arter introdusert i den gamle verden. Arter Cantinoa althaifolia Harley & JFB Pastore Cantinoa americana (Aubl.) Harley & JFB Pastore Cantinoa carpinifolia (Benth.) Harley & JFB Pastore Cantinoa colombiana (Epling) Harley & JFB Pastore Cantinoa dubia Harley & JFBPastore Cantinoa duplicatodentata Harley & JFBPastore Cantinoa erythrostachys (Epling) Harley & JFBPastore Cantinoa heterodon (Epling) Harley & JFBPastore Cantinoa impar (Epling) Harley & JFBPastore Cantinoa indivisa (Pilg.) Harley & JFB Pastore Cantinoa macroptera (Briq.) Harley & JFBPastore Cantinoa multiseta (Benth.) Harley & JFBPastore Cantinoa muricata Harley & JFB Pastore Cantinoa mutabilis (Rich.) Harley & JFB Pastore Cantinoa nanuzae Harley Cantinoa x obvallata (Benth.) Harley & JFB Pastore Cantinoa pinetorum (Epling) Harley & JFBPastore Cantinoa plectranthoides (Benth.) Harley & JFB Pastore Cantinoa propinqua (Epling) Harley & JFBPastore Cantinoa racemulosa Harley & JFB Pastore Cantinoa rubicunda Harley & JFB Pastore Cantinoa similis (Epling) Harley & JFBPastore Cantinoa stricta (Benth.) Harley & JFB Pastore Cantinoa subrotunda Harley & JFB Pastore Cantinoa x sylvularum Harley & JFB Pastore Cantinoa villicaulis (Epling) Harley & JFBPastore Cantinoa violacea Harley & JFB Pastore
Eysines Cantinolle trikkeholdeplass: Eysines Cantinolle trikkeholdeplass er et stopp på Bordeaux -trikken i kommunen Eysines, Frankrike. Det er den nåværende nordvestlige enden av Bordeaux trikkelinje D og åpnet 29. februar 2020.
James Cantion: James Cantion var en irsk rugby union -spiller i London.
James Cantion: James Cantion var en irsk rugby union -spiller i London.
Cantiones sacrae: Cantiones sacrae eller Sacrae cantiones kan referere til: Sacrae cantiones for fire, fem, seks eller flere stemmer , 1573 verk av Alexander Utendal Cantiones quae ab argumento sacrae vocantur , samling fra 1575 av William Byrd og Thomas Tallis Cantiones sacrae , 1589 og 1591 verk av William Byrd Sacrae cantiones liber primus , 1592 verk av Tiburtio Massaino Cantiones sacrae (Gesualdo) , to samlinger av moteter fra Carlo Gesualdo da Venosa utgitt i 1603 Sacrae cantiones , 1614 verk av Vincenzo Ugolini Cantiones sacrae (Schütz) , en samling av førti forskjellige stykker vokal hellig musikk på latinske tekster, komponert av Heinrich Schütz og første gang utgitt i 1625
Carmina Burana (Orff): Carmina Burana er en kantate komponert i 1935 og 1936 av Carl Orff, basert på 24 dikt fra middelaldersamlingen Carmina Burana . Den fulle latinske tittelen er Carmina Burana: Cantiones profanae cantoribus et choris cantandae comitantibus instrumentis atque imaginibus magicis . Den ble først fremført av Oper Frankfurt 8. juni 1937. Den er en del av Trionfi , et musikalsk triptyk som også inkluderer Catulli Carmina og Trionfo di Afrodite . Den første og siste delen av stykket kalles " Fortuna Imperatrix Mundi " og starter med "O Fortuna".
William Byrd: William Byrd var en engelsk komponist fra renessansen. Allment ansett for å være en av de største komponistene i renessansen og en av de største britiske komponistene, hadde han stor innflytelse på komponister både fra hjemlandet England og på kontinentet. Han skrev i mange av skjemaene som var gjeldende i England den gangen, inkludert forskjellige typer hellig og sekulær polyfoni, keyboard og konsortmusikk. Selv om han produserte hellig musikk for anglikanske tjenester, ble han en gang i løpet av 1570 -årene romersk katolikk og skrev katolsk hellig musikk senere i livet.
Cantiones sacrae: Cantiones sacrae eller Sacrae cantiones kan referere til: Sacrae cantiones for fire, fem, seks eller flere stemmer , 1573 verk av Alexander Utendal Cantiones quae ab argumento sacrae vocantur , samling fra 1575 av William Byrd og Thomas Tallis Cantiones sacrae , 1589 og 1591 verk av William Byrd Sacrae cantiones liber primus , 1592 verk av Tiburtio Massaino Cantiones sacrae (Gesualdo) , to samlinger av moteter fra Carlo Gesualdo da Venosa utgitt i 1603 Sacrae cantiones , 1614 verk av Vincenzo Ugolini Cantiones sacrae (Schütz) , en samling av førti forskjellige stykker vokal hellig musikk på latinske tekster, komponert av Heinrich Schütz og første gang utgitt i 1625
Cantiones sacrae (Gesualdo): Sacrae Cantiones fra Carlo Gesualdo da Venosa er to motetsamlinger utgitt i 1603. Det første bindet består av 19 motetter for 5 stemmer, det andre bindet på 20 moteter for 6 eller 7 stemmer. Bassen og seksten i det andre bindet går tapt, men ble rekonstruert av musikkolog James Wood fra 2008 til 2011 og spilt inn av Wood's Vocalconsort Berlin i august 2011.
Cantiones sacrae (Schütz): Cantiones sacrae , Op. 4, er en samling av førti forskjellige stykker vokal hellig musikk på latinske tekster, komponert av Heinrich Schütz og første gang utgitt i 1625. Stykkene har individuelle nummer 53 til 93 i Schütz-Werke-Verzeichnis (SWV), katalogen over hans virker. Den generelle tittelen Cantiones sacrae var vanlig på den tiden og ble brukt av mange komponister, inkludert Palestrina, Byrd og Tallis og Hans Leo Hassler (1591).
Cantiones sacrae (Schütz): Cantiones sacrae , Op. 4, er en samling av førti forskjellige stykker vokal hellig musikk på latinske tekster, komponert av Heinrich Schütz og første gang utgitt i 1625. Stykkene har individuelle nummer 53 til 93 i Schütz-Werke-Verzeichnis (SWV), katalogen over hans virker. Den generelle tittelen Cantiones sacrae var vanlig på den tiden og ble brukt av mange komponister, inkludert Palestrina, Byrd og Tallis og Hans Leo Hassler (1591).
Cantiones sacrae (Schütz): Cantiones sacrae , Op. 4, er en samling av førti forskjellige stykker vokal hellig musikk på latinske tekster, komponert av Heinrich Schütz og første gang utgitt i 1625. Stykkene har individuelle nummer 53 til 93 i Schütz-Werke-Verzeichnis (SWV), katalogen over hans virker. Den generelle tittelen Cantiones sacrae var vanlig på den tiden og ble brukt av mange komponister, inkludert Palestrina, Byrd og Tallis og Hans Leo Hassler (1591).
Cantiorix -inskripsjon: Cantiorix-inskripsjonen er en steingravmarkør for den tidlige post-romerske epoken som ble funnet nær Ffestiniog i Nord-Wales og nå ved kirken i Penmachno. Det er kjent både som den første kjente historiske referansen til kongeriket Gwynedd, og for bruken av de romerske begrepene for 'borger' og 'sorenskriver'.
Cantiorix -inskripsjon: Cantiorix-inskripsjonen er en steingravmarkør for den tidlige post-romerske epoken som ble funnet nær Ffestiniog i Nord-Wales og nå ved kirken i Penmachno. Det er kjent både som den første kjente historiske referansen til kongeriket Gwynedd, og for bruken av de romerske begrepene for 'borger' og 'sorenskriver'.
Cantioscyllium: Cantioscyllium er en utdødd slekt av sykepleierhaier fra mesozoikum. Det er hovedsakelig kjent fra isolerte tenner, men ble navngitt på et delvis skjelett fra slutten av kritt i England. Det er en utbredt og mangfoldig slekt, som for tiden inneholder 10 arter. De er uvanlige, men er tilstede i slutten av kritt i det østlige USA, inkludert Severn Formation of Maryland, Tar Heel og Peedee -formasjonene i North Carolina og Campanian i New Jersey. Det er også kjent fra Western Interior Seaway og Vest -Europa. C. hashimiaensis er kjent fra santoneren i Jordan. C. alhaulfi er fra Barremian.
Cantiq: Cantiq ; en çiberek som er grillet, ikke stekt.
O hellige natt: " O Holy Night " er et velkjent julesang. Opprinnelig basert på et franskspråklig dikt av dikteren Placide Cappeau, skrevet i 1843, med første linje "Minuit, chrétiens! C'est l'heure solennelle" som komponisten Adolphe Adam satte til musikk i 1847. Den engelske versjonen er av John Sullivan Dwight. Julesangen reflekterer over Jesu fødsel som menneskehetens forløsning.
Sveitsisk salme: Den " sveitsiske salmen " er Sveits nasjonalsang.
Cantique de Jean Racine: Cantique de Jean Racine , Op. 11, er en komposisjon for blandet kor og piano eller orgel av Gabriel Fauré. Teksten, "Verbe égal au Très-Haut", er en fransk parafrase av Jean Racine om en latinsk salme fra breviary for matins, Consors paterni luminis . Den nitten år gamle komponisten satte teksten i 1864–65 for en komposisjonskonkurranse på École Niedermeyer de Paris, og den vant ham førstepremien. Verket ble først fremført året etter 4. august 1866 i en versjon med akkompagnement av strykere og orgel. Stilen viser likheter med hans senere verk, Requiem. I dag blir de to verkene ofte fremført sammen.
Cantique de Jean Racine: Cantique de Jean Racine , Op. 11, er en komposisjon for blandet kor og piano eller orgel av Gabriel Fauré. Teksten, "Verbe égal au Très-Haut", er en fransk parafrase av Jean Racine om en latinsk salme fra breviary for matins, Consors paterni luminis . Den nitten år gamle komponisten satte teksten i 1864–65 for en komposisjonskonkurranse på École Niedermeyer de Paris, og den vant ham førstepremien. Verket ble først fremført året etter 4. august 1866 i en versjon med akkompagnement av strykere og orgel. Stilen viser likheter med hans senere verk, Requiem. I dag blir de to verkene ofte fremført sammen.
Cantique de Jean Racine: Cantique de Jean Racine , Op. 11, er en komposisjon for blandet kor og piano eller orgel av Gabriel Fauré. Teksten, "Verbe égal au Très-Haut", er en fransk parafrase av Jean Racine om en latinsk salme fra breviary for matins, Consors paterni luminis . Den nitten år gamle komponisten satte teksten i 1864–65 for en komposisjonskonkurranse på École Niedermeyer de Paris, og den vant ham førstepremien. Verket ble først fremført året etter 4. august 1866 i en versjon med akkompagnement av strykere og orgel. Stilen viser likheter med hans senere verk, Requiem. I dag blir de to verkene ofte fremført sammen.
O hellige natt: " O Holy Night " er et velkjent julesang. Opprinnelig basert på et franskspråklig dikt av dikteren Placide Cappeau, skrevet i 1843, med første linje "Minuit, chrétiens! C'est l'heure solennelle" som komponisten Adolphe Adam satte til musikk i 1847. Den engelske versjonen er av John Sullivan Dwight. Julesangen reflekterer over Jesu fødsel som menneskehetens forløsning.
O hellige natt: " O Holy Night " er et velkjent julesang. Opprinnelig basert på et franskspråklig dikt av dikteren Placide Cappeau, skrevet i 1843, med første linje "Minuit, chrétiens! C'est l'heure solennelle" som komponisten Adolphe Adam satte til musikk i 1847. Den engelske versjonen er av John Sullivan Dwight. Julesangen reflekterer over Jesu fødsel som menneskehetens forløsning.
Cantique de Jean Racine: Cantique de Jean Racine , Op. 11, er en komposisjon for blandet kor og piano eller orgel av Gabriel Fauré. Teksten, "Verbe égal au Très-Haut", er en fransk parafrase av Jean Racine om en latinsk salme fra breviary for matins, Consors paterni luminis . Den nitten år gamle komponisten satte teksten i 1864–65 for en komposisjonskonkurranse på École Niedermeyer de Paris, og den vant ham førstepremien. Verket ble først fremført året etter 4. august 1866 i en versjon med akkompagnement av strykere og orgel. Stilen viser likheter med hans senere verk, Requiem. I dag blir de to verkene ofte fremført sammen.
O hellige natt: " O Holy Night " er et velkjent julesang. Opprinnelig basert på et franskspråklig dikt av dikteren Placide Cappeau, skrevet i 1843, med første linje "Minuit, chrétiens! C'est l'heure solennelle" som komponisten Adolphe Adam satte til musikk i 1847. Den engelske versjonen er av John Sullivan Dwight. Julesangen reflekterer over Jesu fødsel som menneskehetens forløsning.
O hellige natt: " O Holy Night " er et velkjent julesang. Opprinnelig basert på et franskspråklig dikt av dikteren Placide Cappeau, skrevet i 1843, med første linje "Minuit, chrétiens! C'est l'heure solennelle" som komponisten Adolphe Adam satte til musikk i 1847. Den engelske versjonen er av John Sullivan Dwight. Julesangen reflekterer over Jesu fødsel som menneskehetens forløsning.
O hellige natt: " O Holy Night " er et velkjent julesang. Opprinnelig basert på et franskspråklig dikt av dikteren Placide Cappeau, skrevet i 1843, med første linje "Minuit, chrétiens! C'est l'heure solennelle" som komponisten Adolphe Adam satte til musikk i 1847. Den engelske versjonen er av John Sullivan Dwight. Julesangen reflekterer over Jesu fødsel som menneskehetens forløsning.
Cantique des Cantiques: Cantique des cantiques (Song of Songs) er en EP av den franske rockeren Alain Bashung og kona Chloé Mons, utgitt i november 2002 på Barclay Records. De sang begge denne mer enn 25 minutter lange sangen for bryllupet i 2001, på en musikk komponert av Rodolphe Burger og med tekster basert på en ny oversettelse av Bibelens Song of Songs av forfatteren Olivier Cadiot.
Cantique des Cantiques: Cantique des cantiques (Song of Songs) er en EP av den franske rockeren Alain Bashung og kona Chloé Mons, utgitt i november 2002 på Barclay Records. De sang begge denne mer enn 25 minutter lange sangen for bryllupet i 2001, på en musikk komponert av Rodolphe Burger og med tekster basert på en ny oversettelse av Bibelens Song of Songs av forfatteren Olivier Cadiot.
Song of Songs: Song of Songs , også Song of Solomon , Canticle of Canticles , eller Canticles , er en av megillotene (rullene) som ble funnet i den siste delen av Tanakh, kjent som Ketuvim. Den er unik i den hebraiske bibelen: den viser ingen interesse for lov eller pakt eller Israels Gud, og den lærer heller ikke eller utforsker visdom som Ordspråkene eller Forkynneren; i stedet feirer den seksuell kjærlighet, og gir "stemmer fra to elskere, roser hverandre, lengter etter hverandre og gir invitasjoner til å nyte". De to er i harmoni, hver ønsker hverandre og gleder seg over seksuell intimitet; kvinnene i Jerusalem danner et refreng for de elskende, og fungerer som et publikum hvis deltakelse i de elskendes erotiske møter letter leserens deltakelse.
Song of Songs (Giraudoux): Song of Songs er en engelsk bearbeiding av stykket Cantique des Cantiques skrevet i 1938 av den franske dramatikeren Jean Giraudoux.
Song of Songs: Song of Songs , også Song of Solomon , Canticle of Canticles , eller Canticles , er en av megillotene (rullene) som ble funnet i den siste delen av Tanakh, kjent som Ketuvim. Den er unik i den hebraiske bibelen: den viser ingen interesse for lov eller pakt eller Israels Gud, og den lærer heller ikke eller utforsker visdom som Ordspråkene eller Forkynneren; i stedet feirer den seksuell kjærlighet, og gir "stemmer fra to elskere, roser hverandre, lengter etter hverandre og gir invitasjoner til å nyte". De to er i harmoni, hver ønsker hverandre og gleder seg over seksuell intimitet; kvinnene i Jerusalem danner et refreng for de elskende, og fungerer som et publikum hvis deltakelse i de elskendes erotiske møter letter leserens deltakelse.
Kintyre: Kintyre er en halvøy i det vestlige Skottland, sørvest for Argyll og Bute. Halvøya strekker seg omtrent 30 miles, fra Mull of Kintyre i sør til øst og vest Loch Tarbert i nord. Regionen rett nord for Kintyre er kjent som Knapdale.
Çantırlı, Beypazarı: Çantırlı er en landsby i distriktet Beypazarı, Ankara -provinsen, Tyrkia.
Kentish Town: Kentish Town er et område nordvest i London, England i London Borough of Camden, rett nord for Camden Town.
Kentish Town: Kentish Town er et område nordvest i London, England i London Borough of Camden, rett nord for Camden Town.
Kantellert 120-celle: I fire-dimensjonal geometri er en kantellert 120-celle en konveks uniform 4-polytop, som er en kantellasjon av den vanlige 120-cellen.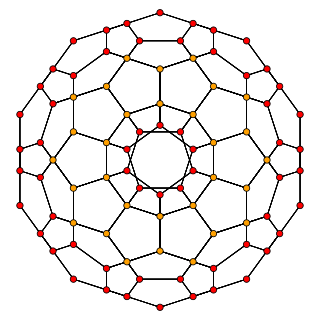
Avkortet 24-celler: I geometri er en avkortet 24-celle en uniform 4-polytop dannet som avkortning av den vanlige 24-cellen.
Cantellated 24-celler: I firdimensjonal geometri er en kantellert 24-celle en konveks uniform 4-polytop, som er en kantellasjon av den vanlige 24-cellen.
Cantitruncated 24-cellers honningkake: I fire-dimensjonal euklidisk geometri er den kantitroniserte 24-cellers honningkake en ensartet romfyllende honningkake. Det kan sees på som en cantitruncation av den vanlige 24-cellers honningkaken, som inneholder avkortede tesseract, cantitruncated 24-cell og tetrahedrale prisme-celler.
Cantellated 5-cellers: I fire-dimensjonal geometri er en kantellert 5-celle en konveks uniform 4-polytop, som er en kantellasjon av den vanlige 5-cellen.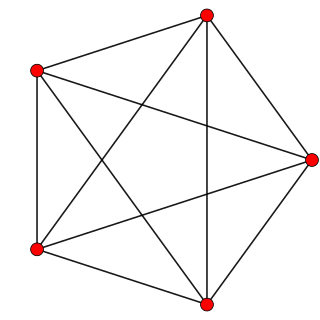
5-cellers honningkake: I den fire-dimensjonale euklidiske geometrien er den 4-simplex honningkake , 5-cellers honningkake eller pentakorisk-dispentakorisk honningkake en romfyllende tessellasjonskake. Den består av 5-celler og rektifiserte 5-cellers fasetter i et forhold på 1: 1.
Cantellated 5-terninger: I seksdimensjonal geometri er en kantellert 5-terning en konveks uniform 5-polytop, som er en kantellasjon av den vanlige 5-terningen.
Runcic 5-terninger: I seksdimensjonal geometri er en runkisk 5-kube eller en konveks uniform 5-polytop. Det er 2 runkiske former for 5-terningen. Runcic 5-terninger har halvparten av hjørnene til runcinated 5-terninger.
Cantellated 5-ortoplexes: I femdimensjonal geometri er en kantellert 5-ortoplex en konveks uniform 5-polytop, som er en kantellasjon av den vanlige 5-ortoplexen.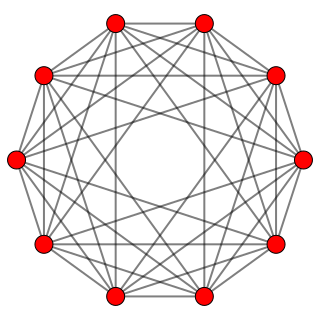
Cantellated 5-simplexer: I femdimensjonal geometri er en kantellert 5-simplex en konveks uniform 5-polytop, som er en kantellasjon av den vanlige 5-simplexen.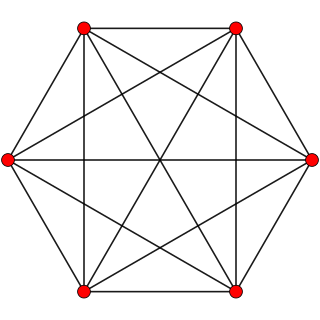
Cantellated 6-terninger: I seksdimensjonal geometri er en kantellert 6-kube en konveks uniform 6-polytop, som er en kantellasjon av den vanlige 6-kuben.
Runcic 6-terninger: I seksdimensjonal geometri er en runkisk 6-kube en konveks uniform 6-polytop. Det er 2 unike runcic for 6-terningen.
Cantellated 6-ortoplexer: I seksdimensjonal geometri er en kantellert 6-ortoplex en konveks uniform 6-polytop, som er en kantellasjon av den vanlige 6-ortoplexen.
Cantellated 6-simplexer: I seksdimensjonal geometri er en kantellert 6-simplex en konveks uniform 6-polytop, som er en kantellasjon av den vanlige 6-simplexen.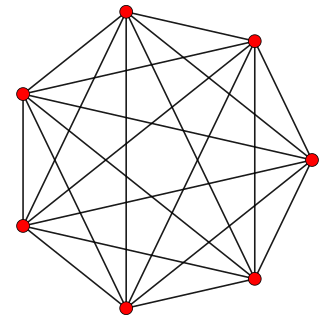
Kantellert 120-celle: I fire-dimensjonal geometri er en kantellert 120-celle en konveks uniform 4-polytop, som er en kantellasjon av den vanlige 120-cellen.
7-terningskanteller: I syvdimensjonal geometri er en kantellert 7-terning en konveks uniform 7-polytop, som er en kantellasjon av den vanlige 7-terningen.
Runcic 7-terninger: I syvdimensjonal geometri er en runkisk 7-kube en konveks uniform 7-polytop, relatert til uniform 7-demicube. Det er 2 unike former.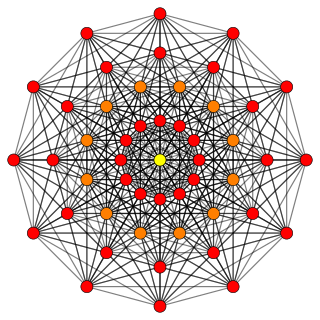
Cantellated 7-ortoplexer: I syvdimensjonal geometri er en kantellert 7-ortoplex en konveks uniform 7-polytop, som er en kantellasjon av den vanlige 7-ortoplexen.
Cantellated 7-simplexer: I syvdimensjonal geometri er en kantellert 7-simplex en konveks uniform 7-polytop, som er en kantellasjon av den vanlige 7-simplexen.
Avkortet tesseract: I geometri er en avkortet tesseract en ensartet 4-polytop dannet som avkortningen av den vanlige tesseracten.
Cantellated 8-simplexer: I åtte-dimensjonal geometri er en kantellert 8-simplex en konveks uniform 8-polytop, som er en kantellasjon av den vanlige 8-simplexen.
Tetrahedral-oktaedrisk honningkake: Den tetraedrisk-oktaedriske bikaken , vekslet kubisk honningkake er en kvasiregulær romfyllende tessellasjon i euklidisk 3-mellomrom. Den består av alternerende vanlige oktaeder og tetraeder i forholdet 1: 2.
Kubisk honningkake: Den kubiske honningkaken eller kubikkcelluleringen er den eneste riktige vanlige romfyllende tessellasjonen i euklidisk 3-rom, som består av kubikkceller. Den har 4 terninger rundt hver kant, og 8 kuber rundt hvert toppunkt. Dens toppunkt er en vanlig oktaeder. Det er en selvdobbel tessellasjon med Schläfli-symbolet {4,3,4}. John Horton Conway kaller denne bikaken en cubille .
Kubisk honningkake: Den kubiske honningkaken eller kubikkcelluleringen er den eneste riktige vanlige romfyllende tessellasjonen i euklidisk 3-rom, som består av kubikkceller. Den har 4 terninger rundt hver kant, og 8 kuber rundt hvert toppunkt. Dens toppunkt er en vanlig oktaeder. Det er en selvdobbel tessellasjon med Schläfli-symbolet {4,3,4}. John Horton Conway kaller denne bikaken en cubille .
Uniform 4-polytop: I geometri er en uniform 4-polytop en 4-dimensjonal polytop som er toppunkt-transitiv og hvis celler er ensartede polyeder, og ansikter er vanlige polygoner.
Sekskantet fliser med honningkake: Innen hyperbolsk geometri er den sekskantede flis-honningkaken en av 11 vanlige parakompakte honningkaker i tredimensjonalt hyperbolsk rom. Det er parakompakt fordi det har celler sammensatt av et uendelig antall ansikter. Hver celle er en sekskantet flislegging hvis hjørner ligger på en horosfære, en overflate i hyperbolsk rom som nærmer seg et enkelt ideelt punkt i det uendelige.
Icosahedral honningkake: Den icosahedral honeycomb er en av fire kompakte vanlige plassfyllende tessellasjoner i hyperbolsk 3-space. Med Schläfli -symbolet {3,5,3} er det tre icosahedra rundt hver kant, og 12 icosahedra rundt hvert toppunkt, i en vanlig dodecahedral toppunktfigur.
Order-4 dodecahedral honeycomb: I geometrien til det hyperbolske 3-rommet er orden-4 dodekaedriske honningkake en av fire kompakte vanlige romfyllende tessellasjoner. Med Schläfli -symbolet {5,3,4} har den fire dodekaeder rundt hver kant, og åtte dodekaeder rundt hvert toppunkt i et oktaedrisk arrangement. Dens hjørner er konstruert av 3 ortogonale akser. Dens doble er ordre-5 kubikk honningkake.
Order-4 sekskantede fliser honningkake: Innen hyperbolsk geometri oppstår orden-4 sekskantede flis-honningkake som en av 11 vanlige parakompakte honningkaker i tredimensjonalt hyperbolsk rom. Det er parakompakt fordi det har celler sammensatt av et uendelig antall ansikter. Hver celle er en sekskantet flis som har hjørner på en horosfære: et flatt plan i hyperbolsk rom som nærmer seg et enkelt ideelt punkt i det uendelige.
Order-4 octahedral honeycomb: Order-4 octahedral honeycomb er en vanlig paracompact honeycomb i hyperbolsk 3-space. Det er parakompakt fordi det har uendelige toppunktfigurer, med alle hjørner som ideelle punkter ved uendelig. Gitt av Schläfli -symbolet {3,4,4}, har den fire ideelle oktaeder rundt hver kant, og uendelig oktaeder rundt hvert toppunkt i en firkantet flisepunkt.
Order-4 square fliser honeycomb: I geometrien til hyperbolsk 3-mellomrom er bestilling-4 kvadratisk flislagt honningkake en av 11 parakompakte vanlige honningkaker. Det er parakompakt fordi det har uendelige celler og toppunktfigurer, med alle hjørner som ideelle punkter ved uendelig. Gitt av Schläfli -symbolet {4,4,4}, har den fire firkantede fliser rundt hver kant og uendelige firkantede fliser rundt hvert toppunkt i en firkantet flisepunkt.
Order-5 cubic honeycomb: Order-5 cubic honeycomb er en av fire kompakte vanlige plassfyllende tessellasjoner i hyperbolsk 3-space. Med Schläfli -symbolet {4,3,5} har det fem kuber {4,3} rundt hver kant og 20 kuber rundt hvert toppunkt. Det er dobbelt med ordre-4 dodekaedriske honningkake.
Order-5 dodecahedral honeycomb: Order-5 dodecahedral honeycomb er en av fire kompakte vanlige romfyllende tessellasjoner i hyperbolsk 3-space. Med Schläfli -symbolet {5,3,5} har den fem dodecahedral -celler rundt hver kant, og hvert toppunkt er omgitt av tjue dodecahedra. Dens toppunkt er en icosahedron.
Order-5 sekskantede fliser honningkake: Innen hyperbolsk geometri oppstår orden-5 sekskantet flis-honningkake som en av 11 vanlige parakompakte honningkaker i tredimensjonalt hyperbolsk rom. Det er parakompakt fordi det har celler sammensatt av et uendelig antall ansikter. Hver celle består av en sekskantet flis som har hjørner på en horosfære, et flatt plan i det hyperbolske rommet som nærmer seg et enkelt ideelt punkt i det uendelige.
Order-6 cubic honeycomb: Order-6 cubic honeycomb er en parakompakt vanlig romfyllende tessellasjon i hyperbolsk 3-space. Det er parakompakt fordi det har toppunktfigurer sammensatt av et uendelig antall fasetter, med alle hjørner som ideelle punkter ved uendelig. Med Schläfli -symbolet {4,3,6} har bikaken seks ideelle terninger som møtes langs hver kant. Dens toppunkt er en uendelig trekantet flislegging. Dens doble er ordre-4 sekskantede fliser honningkake.
Order-6 dodecahedral honeycomb: Order-6 dodecahedral honeycomb er en av 11 parakompakte vanlige honeycombs i hyperbolsk 3-space. Det er parakompakt fordi det har toppunktfigurer sammensatt av et uendelig antall ansikter, med alle hjørner som ideelle punkter ved uendelig. Den har Schläfli -symbolet {5,3,6}, med seks ideelle dodecahedral -celler som omgir hver kant av honningkaken. Hvert toppunkt er ideelt, og omgitt av uendelig mange dodekaeder. Honningkaken har en trekantet flisepunkt.
Order-6 sekskantede fliser honningkake: Innen hyperbolsk geometri er ordre-6 sekskantede fliser honningkake en av 11 vanlige parakompakte honningkaker i tredimensjonalt hyperbolsk rom. Det er parakompakt fordi det har celler med et uendelig antall ansikter. Hver celle er en sekskantet flis som har hjørner på en horosfære: et flatt plan i hyperbolsk rom som nærmer seg et enkelt ideelt punkt i det uendelige.
Order-6 tetrahedral honningkake: I hyperbolsk 3-rom er order-6 tetrahedral honningkake en parakompakt vanlig romfyllende tessellasjon. Det er parakompakt fordi det har toppunktfigurer sammensatt av et uendelig antall ansikter, og har alle hjørner som ideelle punkter ved uendelig. Med Schläfli-symbolet {3,3,6} har order-6 tetraedral honningkake seks ideelle tetraeder rundt hver kant. Alle hjørner er ideelle, med uendelig mange tetraeder som eksisterer rundt hvert toppunkt i en trekantet flisepunkt.
Order-6 tetrahedral honningkake: I hyperbolsk 3-rom er order-6 tetrahedral honningkake en parakompakt vanlig romfyllende tessellasjon. Det er parakompakt fordi det har toppunktfigurer sammensatt av et uendelig antall ansikter, og har alle hjørner som ideelle punkter ved uendelig. Med Schläfli-symbolet {3,3,6} har order-6 tetraedral honningkake seks ideelle tetraeder rundt hver kant. Alle hjørner er ideelle, med uendelig mange tetraeder som eksisterer rundt hvert toppunkt i en trekantet flisepunkt.
Cantellated 5-cellers: I fire-dimensjonal geometri er en kantellert 5-celle en konveks uniform 4-polytop, som er en kantellasjon av den vanlige 5-cellen.
Firkantet fliser honningkake: I geometrien til hyperbolsk 3-mellomrom er den firkantede flisbelegget en av 11 parakompakte vanlige honningkaker. Det kalles parakompakt fordi det har uendelige celler, hvis hjørner eksisterer på horosfærer og konvergerer til et enkelt ideelt punkt i det uendelige. Gitt av Schläfli -symbolet {4,4,3}, har den tre firkantede fliser, {4,4}, rundt hver kant og seks firkantede fliser rundt hvert toppunkt i en kubisk {4,3} toppunkt.
Cantellated tesseract: I fire-dimensjonal geometri er en kantellert tesseract en konveks uniform 4-polytop, som er en kantellasjon av den vanlige tesseracten.
Cantitruncated tesseractic honeycomb: I fire-dimensjonal euklidisk geometri er den kantitroniserte tesseraktiske honningkaken en ensartet romfyllende tessellasjon i euklidisk 4-mellomrom.
Avkortet oktaeder: I geometri er den avkortede oktaeder det arkimediske faststoffet som stammer fra en vanlig oktaeder ved å fjerne seks pyramider, en ved hver av oktaederens hjørner. Den avkortede oktaeder har 14 flater, 36 kanter og 24 hjørner. Siden hver av ansiktene har punktsymmetri, er den avkortede oktaeder et zonoeder. Det er også Goldberg -polyeder G IV (1,1), som inneholder firkantede og sekskantede flater. I likhet med kuben kan den tessellere det tredimensjonale rommet som et permutoeder.
Trekantet fliser honningkake: Den trekantede fliser honningkake er en av 11 parakompakte vanlige romfyllende tessellasjoner i hyperbolsk 3-mellomrom. Det kalles parakompakt fordi det har uendelige celler og toppunktfigurer, med alle hjørner som ideelle punkter ved uendelig. Den har Schläfli -symbolet {3,6,3}, og består av trekantede fliser. Hver kant av bikaken er omgitt av tre celler, og hvert toppunkt er ideelt med uendelig mange celler som møtes der. Dens toppunkt er en sekskantet flis.
Ugrensning: I geometri er en omnitruncation en operasjon som brukes på en vanlig polytop i en Wythoff -konstruksjon som skaper et maksimalt antall fasetter. Det er representert i et Coxeter - Dynkin -diagram med alle noder ringet.
Kent: Kent er et fylke i Sørøst -England og et av hjemfylkene. Det grenser til Stor-London i nord-vest, Surrey i vest og East Sussex i sør-vest, Essex i nord langs elvemunningen til Themsen og det franske departementet Pas-de-Calais. Fylkesbyen er Maidstone.
Cantius: Cantius er en slekt av adapiform primat som bodde i Nord -Amerika og Europa under den tidlige eocen.
Cantius, Cantianus og Cantianilla: Saints Cantius, Cantianus og Cantianilla blir æret som helgener og martyrer av den kristne kirken.
Cantius, Cantianus og Cantianilla: Saints Cantius, Cantianus og Cantianilla blir æret som helgener og martyrer av den kristne kirken.