Cantor (crater)

Cantor (krater): Cantor er et månekollisjonskrater som ligger på den nordlige halvkule på den andre siden av månen. Kraterets ytre kant har en tydelig sekskantet form, og er litt lengre i nord -sør retning. De innvendige veggene er terrasserte, men mindre langs den vestlige kanten. Det er en lav sentral topp i midten av gulvet.
Cantor terning: I matematikk er en Cantor -kube en topologisk gruppe med formen {0, 1} A for et indekssett A. Dens algebraiske og topologiske strukturer er gruppens direkte produkt og produkttopologi over den sykliske gruppen av orden 2.
Cantors diagonale argument: I settteorien ble Cantors diagonale argument , også kalt diagonaliseringsargumentet , det diagonale skråstrekkargumentet , det antidiagonale argumentet , den diagonale metoden og Cantors diagonaliseringsbevis , utgitt i 1891 av Georg Cantor som et matematisk bevis på at det finnes uendelige sett som ikke kan settes i en-til-en-korrespondanse med det uendelige settet med naturlige tall. Slike sett er nå kjent som utallige sett, og størrelsen på uendelige sett blir nå behandlet av teorien om kardinalnummer som Cantor begynte.
Cantors diagonale argument: I settteorien ble Cantors diagonale argument , også kalt diagonaliseringsargumentet , det diagonale skråstrekkargumentet , det antidiagonale argumentet , den diagonale metoden og Cantors diagonaliseringsbevis , utgitt i 1891 av Georg Cantor som et matematisk bevis på at det finnes uendelige sett som ikke kan settes i en-til-en-korrespondanse med det uendelige settet med naturlige tall. Slike sett er nå kjent som utallige sett, og størrelsen på uendelige sett blir nå behandlet av teorien om kardinalnummer som Cantor begynte.
Cantors diagonale argument: I settteorien ble Cantors diagonale argument , også kalt diagonaliseringsargumentet , det diagonale skråstrekkargumentet , det antidiagonale argumentet , den diagonale metoden og Cantors diagonaliseringsbevis , utgitt i 1891 av Georg Cantor som et matematisk bevis på at det finnes uendelige sett som ikke kan settes i en-til-en-korrespondanse med det uendelige settet med naturlige tall. Slike sett er nå kjent som utallige sett, og størrelsen på uendelige sett blir nå behandlet av teorien om kardinalnummer som Cantor begynte.
Cantors diagonale argument: I settteorien ble Cantors diagonale argument , også kalt diagonaliseringsargumentet , det diagonale skråstrekkargumentet , det antidiagonale argumentet , den diagonale metoden og Cantors diagonaliseringsbevis , utgitt i 1891 av Georg Cantor som et matematisk bevis på at det finnes uendelige sett som ikke kan settes i en-til-en-korrespondanse med det uendelige settet med naturlige tall. Slike sett er nå kjent som utallige sett, og størrelsen på uendelige sett blir nå behandlet av teorien om kardinalnummer som Cantor begynte.
Cantors diagonale argument: I settteorien ble Cantors diagonale argument , også kalt diagonaliseringsargumentet , det diagonale skråstrekkargumentet , det antidiagonale argumentet , den diagonale metoden og Cantors diagonaliseringsbevis , utgitt i 1891 av Georg Cantor som et matematisk bevis på at det finnes uendelige sett som ikke kan settes i en-til-en-korrespondanse med det uendelige settet med naturlige tall. Slike sett er nå kjent som utallige sett, og størrelsen på uendelige sett blir nå behandlet av teorien om kardinalnummer som Cantor begynte.
Cantor sett: I matematikk er Cantor -settet et sett med punkter som ligger på et enkelt linjesegment som har en rekke uintuitive egenskaper. Det ble oppdaget i 1874 av Henry John Stephen Smith og introdusert av den tyske matematikeren Georg Cantor i 1883.
Cantor -distribusjon: Cantor -fordelingen er sannsynlighetsfordelingen hvis kumulative fordelingsfunksjon er Cantor -funksjonen.
Cantor sett: I matematikk er Cantor -settet et sett med punkter som ligger på et enkelt linjesegment som har en rekke uintuitive egenskaper. Det ble oppdaget i 1874 av Henry John Stephen Smith og introdusert av den tyske matematikeren Georg Cantor i 1883.
Knaster - Kuratowski -fan: I topologi, en gren av matematikk, er Knaster - Kuratowski -viften et spesifikt forbundet topologisk rom med egenskapen at fjerning av et enkelt punkt gjør det totalt frakoblet. Det er også kjent som Cantors lekkende telt eller Cantors tipi , avhengig av tilstedeværelsen eller fraværet av toppen.
Cantors første settteori -artikkel: Cantors første settteori -artikkel inneholder Georg Cantors første teoremer om transfinitt settteori, som studerer uendelige sett og deres egenskaper. En av disse teoremene er hans "revolusjonerende oppdagelse" om at mengden av alle reelle tall er utallige, snarere enn tellende, uendelige. Denne setningen er bevist ved hjelp av Cantors første utallige bevis , som skiller seg fra det mer kjente beviset ved å bruke hans diagonale argument. Tittelen på artikkelen, " On a Property of the Collection of All Real Algebraic Numbers ", viser til det første teoremet: settet med ekte algebraiske tall er tellbart. Cantors artikkel ble publisert i 1874. I 1879 modifiserte han sitt utallige bevis ved å bruke den topologiske forestillingen om at et sett var tett i et intervall.
Cantor -funksjon: I matematikk er Cantor -funksjonen et eksempel på en funksjon som er kontinuerlig, men ikke absolutt kontinuerlig. Det er et beryktet moteksempel i analyse, fordi det utfordrer naive intuisjoner om kontinuitet, derivat og mål. Selv om den er kontinuerlig overalt og har null derivat nesten overalt, går verdien fortsatt fra 0 til 1 ettersom argumentet når fra 0 til 1. Således virker funksjonen på en måte veldig som en konstant som ikke kan vokse, og i en annen , den vokser faktisk monotont ved konstruksjon.
Kantor i reformjødedom: Kantoren i reformbevegelsen er et presteskap som fyller en mangfoldig rolle i det jødiske samfunnet. Kantorer leder gudstjeneste, driver på livssyklusarrangementer, underviser voksne og barn, driver synagoge musikkprogrammer og tilbyr pastoral omsorg. Kantorer tjener vanligvis sammen med andre geistlige medlemmer, vanligvis rabbinere og noen ganger flere kantorer, i partnerskap for å lede synagogen. Reformkantoren er et profesjonelt kontor med en foreskrevet utdanningsvei og profesjonell organisasjon. Kantorer er "investert", et begrep lånt fra ideen om presteklær, etter avsluttet studie. "Investering" gir status for presteskap til kantorer, akkurat som "ordinasjon" gjør for rabbinere.
Cantors kryssetning: Cantors skjæringssetning refererer til to nært beslektede setninger i generell topologi og reell analyse, oppkalt etter Georg Cantor, om kryss mellom reduserte nestede sekvenser av ikke-tomme kompakte sett.
Knaster - Kuratowski -fan: I topologi, en gren av matematikk, er Knaster - Kuratowski -viften et spesifikt forbundet topologisk rom med egenskapen at fjerning av et enkelt punkt gjør det totalt frakoblet. Det er også kjent som Cantors lekkende telt eller Cantors tipi , avhengig av tilstedeværelsen eller fraværet av toppen.
Cantor -distribusjon: Cantor -fordelingen er sannsynlighetsfordelingen hvis kumulative fordelingsfunksjon er Cantor -funksjonen.
Cantor -medalje: Cantor-medaljen til Deutsche Mathematiker-Vereinigung er oppkalt til ære for Georg Cantor, den første presidenten i samfunnet. Det deles ut maksimalt annethvert år i løpet av de årlige møtene i samfunnet. Prisvinnerne er matematikere som er knyttet til det tyske språket.
Ordinær regning: I det matematiske feltet settteori beskriver ordinal aritmetikk de tre vanlige operasjonene på ordinale tall: addisjon, multiplikasjon og eksponentiering. Hver kan defineres på i hovedsak to forskjellige måter: enten ved å konstruere et eksplisitt velordnet sett som representerer resultatet av operasjonen eller ved å bruke transfinite recursion. Cantors normale form gir en standardisert måte å skrive ordinaler på. I tillegg til disse vanlige ordinære operasjonene, er det også den "naturlige" regning av ordinaler og nimbertoperasjoner.
Paringsfunksjon: I matematikk er en paringsfunksjon en prosess som unikt koder to naturlige tall til et enkelt naturlig tall.
Cantors paradoks: I settteori sier Cantors paradoks at det ikke er et sett med alle kardinaliteter. Dette er avledet fra teoremet om at det ikke er noe størst kardinalnummer. I uformelle termer er paradokset at samlingen av alle mulige "uendelige størrelser" ikke bare er uendelig, men så uendelig stor at dens egen uendelige størrelse ikke kan være noen av de uendelige størrelsene i samlingen. Vanskeligheten håndteres i aksiomatisk settteori ved å erklære at denne samlingen ikke er et sett, men en riktig klasse; i settteorien von Neumann - Bernays - Gödel følger det av dette og aksiomet for størrelsesbegrensning at denne riktige klassen må være i sammenheng med klassen til alle sett. Dermed er det ikke bare uendelig mange uendelig, men denne uendeligheten er større enn noen av uendelighetene den teller.
Cantor sett: I matematikk er Cantor -settet et sett med punkter som ligger på et enkelt linjesegment som har en rekke uintuitive egenskaper. Det ble oppdaget i 1874 av Henry John Stephen Smith og introdusert av den tyske matematikeren Georg Cantor i 1883.
Cantor sett: I matematikk er Cantor -settet et sett med punkter som ligger på et enkelt linjesegment som har en rekke uintuitive egenskaper. Det ble oppdaget i 1874 av Henry John Stephen Smith og introdusert av den tyske matematikeren Georg Cantor i 1883.
Cantor plass: I matematikk er et Cantor -rom , oppkalt etter Georg Cantor, en topologisk abstraksjon av det klassiske Cantor -settet: et topologisk rom er et Cantor -rom hvis det er homeomorft i forhold til Cantor -settet. I mengdelære er topologisk rom 2 ω kalles "the" Cantor plass.
Cantor -funksjon: I matematikk er Cantor -funksjonen et eksempel på en funksjon som er kontinuerlig, men ikke absolutt kontinuerlig. Det er et beryktet moteksempel i analyse, fordi det utfordrer naive intuisjoner om kontinuitet, derivat og mål. Selv om den er kontinuerlig overalt og har null derivat nesten overalt, går verdien fortsatt fra 0 til 1 ettersom argumentet når fra 0 til 1. Således virker funksjonen på en måte veldig som en konstant som ikke kan vokse, og i en annen , den vokser faktisk monotont ved konstruksjon.
Knaster - Kuratowski -fan: I topologi, en gren av matematikk, er Knaster - Kuratowski -viften et spesifikt forbundet topologisk rom med egenskapen at fjerning av et enkelt punkt gjør det totalt frakoblet. Det er også kjent som Cantors lekkende telt eller Cantors tipi , avhengig av tilstedeværelsen eller fraværet av toppen.
Cantor -funksjon: I matematikk er Cantor -funksjonen et eksempel på en funksjon som er kontinuerlig, men ikke absolutt kontinuerlig. Det er et beryktet moteksempel i analyse, fordi det utfordrer naive intuisjoner om kontinuitet, derivat og mål. Selv om den er kontinuerlig overalt og har null derivat nesten overalt, går verdien fortsatt fra 0 til 1 ettersom argumentet når fra 0 til 1. Således virker funksjonen på en måte veldig som en konstant som ikke kan vokse, og i en annen , den vokser faktisk monotont ved konstruksjon.
Cantor sett: I matematikk er Cantor -settet et sett med punkter som ligger på et enkelt linjesegment som har en rekke uintuitive egenskaper. Det ble oppdaget i 1874 av Henry John Stephen Smith og introdusert av den tyske matematikeren Georg Cantor i 1883.
Cantors teorem: I elementær settteori er Cantors teorem et grunnleggende resultat som sier at for ethvert sett , settet til alle delsettene av har en strengt større kardinalitet enn seg selv. For endelige sett kan Cantors teorem ses å være sant ved enkel oppregning av antall undersett. Teller det tomme settet som et delsett, et sett med medlemmer har totalt delsett, slik at hvis deretter , og teoremet holder fordi for alle ikke-negative heltall.
Cantor plass: I matematikk er et Cantor -rom , oppkalt etter Georg Cantor, en topologisk abstraksjon av det klassiske Cantor -settet: et topologisk rom er et Cantor -rom hvis det er homeomorft i forhold til Cantor -settet. I mengdelære er topologisk rom 2 ω kalles "the" Cantor plass.
Cantor tree: I matematisk settteori er Cantor -treet enten det fulle binære treet i høyden ω + 1, eller et topologisk rom relatert til dette ved å kombinere sine poeng med intervaller, som ble introdusert av Robert Lee Moore på slutten av 1920 -tallet som et eksempel på en ikke-metrerbart Moore-rom.
Cantor tree overflate: I dynamiske systemer er Cantor-treet en uendelig slektsoverflate som er homeomorf til en sfære med et Cantorsett fjernet. Det blomstrende Cantor -treet er et Cantor -tre med et uendelig antall håndtak lagt til på en slik måte at hver ende er en grense for håndtak.
Cantor sett: I matematikk er Cantor -settet et sett med punkter som ligger på et enkelt linjesegment som har en rekke uintuitive egenskaper. Det ble oppdaget i 1874 av Henry John Stephen Smith og introdusert av den tyske matematikeren Georg Cantor i 1883.
Cantora 1: Cantora 1 er et studioalbum av den avdøde argentinske sangeren Mercedes Sosa. Den ble utgitt i 2009 og inneholder duetter med fremtredende latinamerikanske innspillingsartister. Det ble sertifisert platina av CAPIF. Dette betyr at albumet solgte 40 000 eksemplarer i Argentina.
Cantora Records: Cantora Records er et Brooklyn-basert uavhengig plateselskap, mest kjent for å signere det psykedeliske popbandet MGMT og utstede bandets første kommersielle utgivelse, Time to Pretend .
Hazzan: En hazzan eller chazzan er en jødisk musiker eller forløper utdannet i vokalkunsten som hjelper til med å lede menigheten i sangfull bønn. På engelsk blir denne bønnelederen ofte referert til som en kantor , et begrep som også brukes i kristendommen.
Cantorchilus: Cantorchilus er en slekt av fugler i wren -familien. Etablert av Nigel I. Mann, F. Keith Barker, Jeff A. Graves, Kimberly A. Dingess-Mann og Peter JB Slater i 2006, og inneholder 10 arter. Alle artene som ble tildelt den var tidligere inkludert i slekten Thryothorus .
Isthmian wren: Den ismiske wren er en fuglearte i familien Troglodytidae. Den finnes i Costa Rica og Panama.
Grå syre: Den grå myren er en fugleart i familien Troglodytidae. Det er endemisk i den sørvestlige delen av Amazonas -staten i Brasil. Denne lille, dårlig kjente myren ligner noe på en hagesnurr, men den øvre delen er grå.
Fawn-breasted wren: Den fawn-breasted wren er en fugleart i familien Troglodytidae. Den finnes i Bolivia, Brasil og Paraguay.
Strip-throated wren: Den stripete halsen er en fugleart i familien Troglodytidae. Den finnes i Colombia, Ecuador og Panama.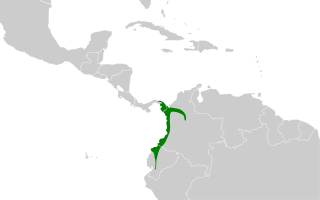
Buff-breasted wren: Den buff-breasted wren er en fugleart i familien Troglodytidae. Den finnes i Amazonas-bassenget i Nord-Brasil og Amazonas Colombia, Ecuador, Peru og nordlige grensen til Bolivia, og også Guyana-landene Guyana, Surinam og Fransk Guyana. Det forekommer i ikke-Amazonas-regioner i Venezuela og Colombia, og området strekker seg til det østlige Panama.
Long-billed wren: Den langnebbede wren er en fugleart i familien Troglodytidae. Det er endemisk for Brasil.
Cabanis's wren: Cabanis's wren er en fugleart i familien Troglodytidae. Den finnes i Belize, Costa Rica, El Salvador, Guatemala, Honduras, Mexico og Nicaragua.
Bay wren: Bay wren er en fugleart i familien Troglodytidae. Det er hjemmehørende i Sør -Mellom -Amerika og nordvest i Sør -Amerika.
Riverside wren: Elvebredden er en fugleart i familien Troglodytidae. Den finnes i Costa Rica og Panama.
Superciliated wren: Den superciliated wren er en fugleart i familien Troglodytidae. Den finnes i Ecuador og Peru.
Stripe-breasted wren: Den stripe-breasted wren er en fugleart i familien Troglodytidae. Den finnes i Honduras, Nicaragua, Costa Rica og Panama.
Canebrake wren: Canebrake wren er en fugleart i familien Troglodytidae. Den finnes i Costa Rica, Nicaragua og Panama.
Cantore al liuto: Cantore al liuto - typisk italiensk definisjon for musikere og komponister i slutten av 1400 - er den sangende lutisten hvis beskrivelse og historiske representasjon er dypt forankret i fortiden som går tilbake til myten om Orfeus.
Batagur: Batagur er en slekt med store skilpadder fra Sør- og Sørøst -Asia. Alle medlemmer av slekten er alvorlig truet. Med en nylig fusjon med medlemmer fra to andre slekter, har denne slekten seks beskrevne arter.
Cantores minores: Cantores Minores er et kor i Helsingfors katedral, og Finlands eldste og mest vellykkede guttekor. Beskytter for koret er Finlands president. Koret består av rundt tre hundre 4- til 25 år gamle gutter og unge menn.
Cantores Minores (Warszawa): Cantores Minores er et polsk mannlig kor som ble opprettet i 1990 og tilknyttet St. John's Archcathedral i Warszawa.
Cantores minores: Cantores Minores er et kor i Helsingfors katedral, og Finlands eldste og mest vellykkede guttekor. Beskytter for koret er Finlands president. Koret består av rundt tre hundre 4- til 25 år gamle gutter og unge menn.
Cantores Minores (Warszawa): Cantores Minores er et polsk mannlig kor som ble opprettet i 1990 og tilknyttet St. John's Archcathedral i Warszawa.
Cantoria: Cantoria er en kommune i Almería -provinsen, i det autonome samfunnet Andalucía, Spania.
Cantoria: Cantoria er en kommune i Almería -provinsen, i det autonome samfunnet Andalucía, Spania.
Cantoria: Cantoria er en kommune i Almería -provinsen, i det autonome samfunnet Andalucía, Spania.
Cantoria: Cantoria er en kommune i Almería -provinsen, i det autonome samfunnet Andalucía, Spania.
Cantoria violacea: Cantoria violacea , kjent som Cantors vannslange , er en slangeart som finnes i tropisk Asia. Det er oppkalt etter ære for 1800 -tallets herpetolog Theodore Cantor.
Ron Carpenter (designer): Ron Carpenter er en engelsk typograf. Han ble utdannet som kartograf og ble senere en skriftdesigner. Han jobber for uavhengig skriftstøperi, Dalton Maag.
Cantoria violacea: Cantoria violacea , kjent som Cantors vannslange , er en slangeart som finnes i tropisk Asia. Det er oppkalt etter ære for 1800 -tallets herpetolog Theodore Cantor.
Georg Cantor: Georg Ferdinand Ludwig Philipp Cantor var en tysk matematiker. Han skapte settteori, som har blitt en grunnleggende teori i matematikk. Cantor fastslår viktigheten av en-til-en-korrespondanse mellom medlemmene i to sett, definerte uendelige og velordnede sett, og beviste at de reelle tallene er flere enn de naturlige tallene. Faktisk innebærer Cantors metode for bevis på denne teoremet eksistensen av en uendelighet av uendelige. Han definerte kardinal- og ordinaltall og aritmetikken deres. Cantors arbeid er av stor filosofisk interesse, et faktum han var godt klar over.
Cantorion Colin Jones: Cantorion Colin Jones var et walisisk mannskonsertkor. Koret ble grunnlagt av Colin Jones 1. september 1991 på et møte i Lecture Theatre, ved Plas Coch College og sammensatt av sangere som Colin tidligere hadde undervist og dirigert i kor i Nord -Wales.
Cantoris: Cantoris er siden av et kirkekor okkupert av Cantor. I engelske kirker er dette vanligvis korstallene på nordsiden av koret, selv om det er noen bemerkelsesverdige unntak, for eksempel Durham Cathedral, Ely Cathedral, Carlisle Cathedral og Southwell Minster. Den motsatte siden er kjent som decani, som er der dekanen satt.
Georg Cantor: Georg Ferdinand Ludwig Philipp Cantor var en tysk matematiker. Han skapte settteori, som har blitt en grunnleggende teori i matematikk. Cantor fastslår viktigheten av en-til-en-korrespondanse mellom medlemmene i to sett, definerte uendelige og velordnede sett, og beviste at de reelle tallene er flere enn de naturlige tallene. Faktisk innebærer Cantors metode for bevis på denne teoremet eksistensen av en uendelighet av uendelige. Han definerte kardinal- og ordinaltall og aritmetikken deres. Cantors arbeid er av stor filosofisk interesse, et faktum han var godt klar over.
Mauro Cantoro: Roberto Mauro Cantoro , kallenavnet El Toro , er en argentinsk fotballspiller, som spiller for León de Huánuco.
Cantor: En kantor eller chanter er en person som fører folk i sang eller noen ganger i bønn. I formell kristen tilbedelse er en kantor en person som synger solovers eller passasjer som koret eller menigheten reagerer på.
Cantors Assembly: Cantors Assembly (CA) er den internasjonale sammenslutningen av hazzanim (kantorer) tilknyttet konservativ jødedom. Cantors Assembly ble grunnlagt i 1947 for å utvikle yrket til hazzan, for å fremme hazzanimers fellesskap og velferd og for å etablere et vinterhage for hazzanim. Sistnevnte mål ble realisert i 1952 med etableringen av Cantors Institute ved the Jewish Theological Seminary of America. Dette instituttet utviklet seg senere til HL Miller Cantorial School of the Jewish Theological Seminary of America.
Cantors diagonale argument: I settteorien ble Cantors diagonale argument , også kalt diagonaliseringsargumentet , det diagonale skråstrekkargumentet , det antidiagonale argumentet , den diagonale metoden og Cantors diagonaliseringsbevis , utgitt i 1891 av Georg Cantor som et matematisk bevis på at det finnes uendelige sett som ikke kan settes i en-til-en-korrespondanse med det uendelige settet med naturlige tall. Slike sett er nå kjent som utallige sett, og størrelsen på uendelige sett blir nå behandlet av teorien om kardinalnummer som Cantor begynte.
Cantors kryssetning: Cantors skjæringssetning refererer til to nært beslektede setninger i generell topologi og reell analyse, oppkalt etter Georg Cantor, om kryss mellom reduserte nestede sekvenser av ikke-tomme kompakte sett.
Cantors kryssetning: Cantors skjæringssetning refererer til to nært beslektede setninger i generell topologi og reell analyse, oppkalt etter Georg Cantor, om kryss mellom reduserte nestede sekvenser av ikke-tomme kompakte sett.
Cantors teorem: I elementær settteori er Cantors teorem et grunnleggende resultat som sier at for ethvert sett , settet til alle delsettene av har en strengt større kardinalitet enn seg selv. For endelige sett kan Cantors teorem ses å være sant ved enkel oppregning av antall undersett. Teller det tomme settet som et delsett, et sett med medlemmer har totalt delsett, slik at hvis deretter , og teoremet holder fordi for alle ikke-negative heltall.
Avledet sett (matematikk): I matematikk, nærmere bestemt i punkt-sett topologi, det avledede settet til et delsett av et topologisk rom er settet med alle grensepunkter for Det er vanligvis betegnet med
Avledet sett (matematikk): I matematikk, nærmere bestemt i punkt-sett topologi, det avledede settet til et delsett av et topologisk rom er settet med alle grensepunkter for Det er vanligvis betegnet med
Perfekt sett eiendom: I beskrivende settteori har en delmengde av et polsk mellomrom den perfekte settegenskapen hvis den enten kan telles eller har en perfekt undermengde. Vær oppmerksom på at det å ha den perfekte settegenskapen ikke er det samme som å være et perfekt sett.
Cantor - Bernstein setning: I settteori og ordensteori uttaler Cantor - Bernstein -setningen at kardinaliteten til den andre typeklassen, klassen av tellbare ordenstyper, er lik kardinaliteten til kontinuumet. Den ble brukt av Felix Hausdorff og oppkalt av ham etter Georg Cantor og Felix Bernstein. Cantor konstruerte en familie av utallige ordenstyper med kardinaliteten i kontinuumet, og i hans første avhandling fra 1901 beviste Bernstein at en slik familie ikke kan ha høyere kardinalitet.
Schröder - Bernstein teorem: I settteori sier Schröder - Bernstein -teoremet at hvis det eksisterer injeksjonsfunksjoner f : A → B og g : B → A mellom settene A og B , eksisterer det en bijektiv funksjon h : A → B.
Schröder - Bernstein teorem: I settteori sier Schröder - Bernstein -teoremet at hvis det eksisterer injeksjonsfunksjoner f : A → B og g : B → A mellom settene A og B , eksisterer det en bijektiv funksjon h : A → B.
Schröder - Bernstein teorem: I settteori sier Schröder - Bernstein -teoremet at hvis det eksisterer injeksjonsfunksjoner f : A → B og g : B → A mellom settene A og B , eksisterer det en bijektiv funksjon h : A → B.
Axor for Cantor - Dedekind: I matematisk logikk er Cantor-Dedekind-aksiomet tesen om at de reelle tallene er orden-isomorfe i forhold til det lineære kontinuumet i geometri. Med andre ord sier aksiomet at det er en en-til-en-korrespondanse mellom reelle tall og punkter på en linje.
Cantor -funksjon: I matematikk er Cantor -funksjonen et eksempel på en funksjon som er kontinuerlig, men ikke absolutt kontinuerlig. Det er et beryktet moteksempel i analyse, fordi det utfordrer naive intuisjoner om kontinuitet, derivat og mål. Selv om den er kontinuerlig overalt og har null derivat nesten overalt, går verdien fortsatt fra 0 til 1 ettersom argumentet når fra 0 til 1. Således virker funksjonen på en måte veldig som en konstant som ikke kan vokse, og i en annen , den vokser faktisk monotont ved konstruksjon.
Schröder - Bernstein teorem: I settteori sier Schröder - Bernstein -teoremet at hvis det eksisterer injeksjonsfunksjoner f : A → B og g : B → A mellom settene A og B , eksisterer det en bijektiv funksjon h : A → B.
Schröder - Bernstein teorem: I settteori sier Schröder - Bernstein -teoremet at hvis det eksisterer injeksjonsfunksjoner f : A → B og g : B → A mellom settene A og B , eksisterer det en bijektiv funksjon h : A → B.
Cantor - Zassenhaus algoritme: I beregningsalgebra er Cantor - Zassenhaus -algoritmen en metode for faktorisering av polynomer over begrensede felt.
Cantor - Zassenhaus algoritme: I beregningsalgebra er Cantor - Zassenhaus -algoritmen en metode for faktorisering av polynomer over begrensede felt.
Asiatisk gigantisk softshell skilpadde: Den asiatiske gigantiske softshell-skilpadden , også kjent som Cantors gigantiske softshell-skilpadde og den froskeansiktede softshell-skilpadden , er en art av ferskvannsskilpadde i familien Trionychidae. Arten er hjemmehørende i Sørøst -Asia. Arten er truet og har på 1900 -tallet forsvunnet fra store deler av sin tidligere rekkevidde.
Asiatisk gigantisk softshell skilpadde: Den asiatiske gigantiske softshell-skilpadden , også kjent som Cantors gigantiske softshell-skilpadde og den froskeansiktede softshell-skilpadden , er en art av ferskvannsskilpadde i familien Trionychidae. Arten er hjemmehørende i Sørøst -Asia. Arten er truet og har på 1900 -tallet forsvunnet fra store deler av sin tidligere rekkevidde.
Asiatisk gigantisk softshell skilpadde: Den asiatiske gigantiske softshell-skilpadden , også kjent som Cantors gigantiske softshell-skilpadde og den froskeansiktede softshell-skilpadden , er en art av ferskvannsskilpadde i familien Trionychidae. Arten er hjemmehørende i Sørøst -Asia. Arten er truet og har på 1900 -tallet forsvunnet fra store deler av sin tidligere rekkevidde.
Cantos: Cantos av Ezra Pound er et langt, ufullstendig dikt i 116 seksjoner, som hver er en kanto . Det meste ble skrevet mellom 1915 og 1962, selv om mye av det tidlige arbeidet ble forlatt og de tidlige kantosene, som endelig ble publisert, stammer fra 1922 og fremover. Det er et boklengdeverk, allment ansett for å være en intens og utfordrende lesning. Cantos regnes generelt som et av de mest betydningsfulle verker av modernistisk poesi på 1900 -tallet. Som i Pounds prosaskriving er temaene økonomi, styring og kultur integrert i verkets innhold.
Cantos Aztecas: Cantos Aztecas er et album med sanger fra 1988 på aztekisk språk komponert av Lalo Schifrin og sunget av Plácido Domingo.
Bernardo Guimarães: Bernardo Joaquim da Silva Guimarães var en brasiliansk poet og romanforfatter. Han er forfatteren av de berømte romansene A Escrava Isaura og O Seminarista . Han introduserte også for brasiliansk poesi verso bestialógico , også referert til som pantagruélico - dikt hvis vers er veldig meningsløse, men veldig metriske. Under verso bestialógico skrev han polemiske erotiske vers, for eksempel "O Elixir do Pajé" og "A Origem do Mênstruo". Et ikke-erotisk dikt skrevet verso bestialógico er "Eu Vi dos Polos o Gigante Alado".
Love Songs (Gipsy Kings album): Love Songs er et "best of" -album av det franske Rumba Catalana -bandet Gipsy Kings, som ble utgitt i 1996. Den inkluderer den nye uutgitte sangen "Gitano Soy". En amerikansk utgivelse av dette albumet ble gitt ut i 1998 for et amerikansk publikum under navnet Cantos de Amor .
Chants d'Espagne: Chants d'Espagne , Op. 232, er en suite med opprinnelig tre, senere fem stykker for pianoet av Isaac Albéniz. Prélude , Orientale og Sous le palmier ble utgitt i 1892, og Córdoba og Seguidillas ble lagt til i 1898 -utgaven. I følge Günter Schulze, "Mange ... [av verkene] har smaken av flamencoen som er så elsket av Albéniz." [1]
Chants d'Espagne: Chants d'Espagne , Op. 232, er en suite med opprinnelig tre, senere fem stykker for pianoet av Isaac Albéniz. Prélude , Orientale og Sous le palmier ble utgitt i 1892, og Córdoba og Seguidillas ble lagt til i 1898 -utgaven. I følge Günter Schulze, "Mange ... [av verkene] har smaken av flamencoen som er så elsket av Albéniz." [1]
Cantos nacionales: Cantos nacionales ("nasjonale sanger" eller "nasjonalistiske sanger" var tre sanger fra den spanske borgerkrigen som ble anerkjent av frankoistiske Spania for å hedre de falne. Dekret 226/1937 fra Burgos Junta erklærte Marcha Granadera som den spanske hymnen. Den anerkjenner også som cantos nacionales sanger av Falange Española, Carlism og den spanske legionen som beordret at de skulle lyttes til å stå i hyllest til fedrelandet og de falne. Et dekret fra 1942 gjeninnfører sangene og beordrer at, i offisielle hendelser, spillingen av hymnen og sangene må hilses med en "nasjonalhilsen", eller en militærhilsen hvis hendelsen utelukkende er militær.
Cantos: Cantos av Ezra Pound er et langt, ufullstendig dikt i 116 seksjoner, som hver er en kanto . Det meste ble skrevet mellom 1915 og 1962, selv om mye av det tidlige arbeidet ble forlatt og de tidlige kantosene, som endelig ble publisert, stammer fra 1922 og fremover. Det er et boklengdeverk, allment ansett for å være en intens og utfordrende lesning. Cantos regnes generelt som et av de mest betydningsfulle verker av modernistisk poesi på 1900 -tallet. Som i Pounds prosaskriving er temaene økonomi, styring og kultur integrert i verkets innhold.
Cantos of the Kalevala: Dette er et sammendrag av kantoene i Kalevala .
Liste over kratere på Mars: A – G: Dette er en delvis liste over kratere på Mars. Det er hundretusener av nedslagskratere på Mars, men bare noen av dem har navn. Denne listen her inneholder bare navngitte Mars -kratere som begynner med bokstaven A - G (se også lister for H - N og O - Z) .
Liste over kratere på Mars: A – G: Dette er en delvis liste over kratere på Mars. Det er hundretusener av nedslagskratere på Mars, men bare noen av dem har navn. Denne listen her inneholder bare navngitte Mars -kratere som begynner med bokstaven A - G (se også lister for H - N og O - Z) .
Cantown, Casey County, Kentucky: Cantown er et ikke- inkorporert samfunn i Casey County, Kentucky, USA. Det ble også kjent som Contown .
Cantrainea: Cantrainea er en slekt av sjøsnegler, marine gastropodbløtdyr i familien Colloniidae.
Cantrainea alfi: Cantrainea alfi er en art av havsnegl, en marin gastropod -bløtdyr i familien Colloniidae.
Cantrainea globuloides: Cantrainea globuloides er en art av havsnegl, en marin gastropod -bløtdyr i familien Colloniidae.
Cantrainea indica: Cantrainea indica er en art av liten havsnegl med kalkholdig opercula, en marin gastropod -bløtdyr i familien Colloniidae.
Cantrainea inexpectata: Cantrainea inexpectata er en art av liten havsnegl med kalkholdig opercula, en marin gastropod -bløtdyr i familien Colloniidae.
Cantrainea jamsteci: Cantrainea jamsteci er en art av liten sjøsnegl med kalkholdig opercula, en marin gastropod -bløtdyr i familien Colloniidae.
Cantrainea macleani: Cantrainea macleani er en art av havsnegl, en marin gastropod -bløtdyr i familien Colloniidae.
Cantrainea nuda: Cantrainea nuda er en art av havsnegl, en marin gastropod -bløtdyr i familien Colloniidae.
Cantrainea panamensis: Cantrainea panamensis er en art av liten sjøsnegl med kalkholdig opercula, en marin gastropod -bløtdyr i familien Colloniidae.
Cantrainea peloritana: Cantrainea peloritana er en art av sjøsnegl, en marin gastropod -bløtdyr i familien Colloniidae.
Cantrainea philipiana: Cantrainea philipiana er en art av liten havsnegl med kalkholdig opercula, en marin gastropod -bløtdyr i familien Colloniidae.
Cantrainea sunderlandi: Cantrainea sunderlandi er en art av liten havsnegl med kalkholdig opercula, en marin gastropod -bløtdyr i familien Colloniidae.
Cantrainea yoyottei: Cantrainea yoyottei er en art av havsnegl, en marin gastropod -bløtdyr i familien Colloniidae.
Cantrall, Illinois: Cantrall er en landsby i Sangamon County, Illinois, USA. Befolkningen var 139 ved folketellingen i 2000. Det er en del av Springfield, Illinois Metropolitan Statistical Area.
Liodessus cantralli: Liodessus cantralli , eller Cantralls myrbille , er en art av predative dykkebille i familien Dytiscidae. Den finnes i Nord -Amerika.
Cantrall, Illinois: Cantrall er en landsby i Sangamon County, Illinois, USA. Befolkningen var 139 ved folketellingen i 2000. Det er en del av Springfield, Illinois Metropolitan Statistical Area.
Cantrall, Illinois: Cantrall er en landsby i Sangamon County, Illinois, USA. Befolkningen var 139 ved folketellingen i 2000. Det er en del av Springfield, Illinois Metropolitan Statistical Area.
Cantre'r Gwaelod: Cantre'r Gwaelod , også kjent som Cantref Gwaelod eller Cantref y Gwaelod , er et legendarisk gammelt senket rike som sies å ha okkupert et område med fruktbart land som ligger mellom Ramsey Island og Bardsey Island i det som nå er Cardigan Bay vest for Wales. Det har blitt beskrevet som en "walisisk Atlantis" og har omtalt i folklore, litteratur og sang.
Inngår: A cantred var en underavdeling av et fylke i det anglo-normanniske herredømmet i Irland mellom det trettende og femtende århundre, analogt med cantref of Wales eller hundrevis av England. I County Dublin tilsvarende enheten ble kalt en serjeanty, mens i County Meath og environs det var en baroniet. Området til en cantred tilsvarte vanligvis området til en tidligere trícha cét fra det gæliske Irland, og noen ganger til et landlig dekan i den middelalderske irske kirken. Paul Mac Cotter har "demonstrert eksistensen av 151 visse kantreder og indikert den sannsynlige eksistensen av ytterligere 34." Cantreds ble erstattet av baroner fra det sekstende århundre.
Cantred (disambiguation): A cantred var en underavdeling av et fylke i Irland på 1200- til 1500 -tallet.