Geometric mean

Geometrisk gjennomsnitt: I matematikk er det geometriske gjennomsnittet et gjennomsnitt eller gjennomsnitt, som indikerer den sentrale tendensen eller den typiske verdien til et sett med tall ved å bruke produktet av deres verdier. Den geometriske middelverdi er definert som den n-te rot av produktet av n antall, det vil si, for et sett med tall x 1, X2, ..., Xn, det geometriske gjennomsnittet er definert som
Logaritmisk gjennomsnitt: I matematikk er det logaritmiske gjennomsnittet en funksjon av to ikke-negative tall som er lik forskjellen delt på logaritmen til kvotienten. Denne beregningen gjelder i tekniske problemer som involverer varme og masseoverføring.
Aritmetisk logikkenhet: I databehandling er en aritmetisk logisk enhet (ALU) en kombinasjons digital krets som utfører aritmetiske og bitvise operasjoner på heltall binære tall. Dette er i motsetning til en flytende punktenhet (FPU), som opererer på flytende nummer. Det er en grunnleggende byggestein for mange typer datakretser, inkludert den sentrale prosessorenheten (CPU) på datamaskiner, FPUer og grafikkbehandlingsenheter (GPUer).
Aritmetikk (sang): " Arithmetic " er en singel av Brooke Fraser utgitt i 2004. Sangen er første spor av Frasers debutalbum What to Do with Daylight . Sangen ble senere inkludert i Sony BMG-samlingen More Nature , en samling av sanger fra New Zealand Sony BMG-katalogen.
Aritmetikk (sang): " Arithmetic " er en singel av Brooke Fraser utgitt i 2004. Sangen er første spor av Frasers debutalbum What to Do with Daylight . Sangen ble senere inkludert i Sony BMG-samlingen More Nature , en samling av sanger fra New Zealand Sony BMG-katalogen.
Aritmetisk logikkenhet: I databehandling er en aritmetisk logisk enhet (ALU) en kombinasjons digital krets som utfører aritmetiske og bitvise operasjoner på heltall binære tall. Dette er i motsetning til en flytende punktenhet (FPU), som opererer på flytende nummer. Det er en grunnleggende byggestein for mange typer datakretser, inkludert den sentrale prosessorenheten (CPU) på datamaskiner, FPUer og grafikkbehandlingsenheter (GPUer).
Aritmetisk geometri: I matematikk er aritmetisk geometri omtrent anvendelse av teknikker fra algebraisk geometri til problemer i tallteori. Aritmetisk geometri er sentrert rundt Diophantine geometry, studiet av rasjonelle punkter av algebraiske varianter.
Arakelov teori: I matematikk er Arakelov-teorien en tilnærming til diofantinsk geometri, oppkalt etter Suren Arakelov. Den brukes til å studere diofantiske ligninger i høyere dimensjoner.
Aritmetisk koding: Aritmetisk koding ( AC ) er en form for entropikoding som brukes i tapsfri datakomprimering. Normalt blir en streng med tegn som ordene "hallo der" representert ved hjelp av et fast antall bits per tegn, som i ASCII-koden. Når en streng konverteres til aritmetisk koding, lagres ofte brukte tegn med færre biter, og ikke så ofte forekommende tegn lagres med flere biter, noe som resulterer i færre biter som brukes totalt. Aritmetisk koding skiller seg fra andre former for entropikoding, for eksempel Huffman-koding, ved at i stedet for å skille inngangen i komponentsymboler og erstatte hver med en kode, koder aritmetisk koding hele meldingen til et enkelt tall, en vilkårlig presisjonsfraksjon q , hvor 0,0 ≤ q <1,0 . Den representerer gjeldende informasjon som et område, definert av to tall. En nylig familie av entropikodere kalt asymmetriske tallsystemer muliggjør raskere implementeringer takket være direkte drift på et enkelt naturlig tall som representerer gjeldende informasjon.
Regning og geometrisk Frobenius: I matematikk er Frobenius-endomorfismen definert i hvilken som helst kommutativ ring R som har karakteristisk p , hvor p er et primtall. Kartleggingen φ som tar r i R til r p er nemlig en ringendomorfisme av R.
Frobenius endomorfisme: I kommutativ algebra og feltteori er Frobenius endomorfisme en spesiell endomorfisme av kommutative ringer med hovedkarakteristikk p , en viktig klasse som inkluderer endelige felt. Den endomorphism kartene hvert element til sin p -te makt. I visse sammenhenger er det en automorfisme, men dette stemmer ikke generelt.
Aritmetisk fuchsisk gruppe: Aritmetiske fuchsiske grupper er en spesiell klasse av fuchsiske grupper konstruert ved bruk av ordrer i kvaternionsalgebras. De er spesielle forekomster av aritmetiske grupper. Det prototypiske eksemplet på en aritmetisk Fuchsian-gruppe er modulgruppen . De og den hyperbolske overflaten assosiert med deres virkning på det hyperbolske planet viser ofte spesielt regelmessig oppførsel blant fuchsiske grupper og hyperbolske overflater.
Diofantinligning: I matematikk er en diofantisk ligning en polynomligning, som vanligvis involverer to eller flere ukjente, slik at de eneste løsningene av interesse er heltallene. En lineær diofantinligning tilsvarer en konstant summen av to eller flere monomier, hver av grad en. En eksponentiell diofantinligning er en der ukjente kan vises i eksponenter.
Aritmetikk IF: Den aritmetiske IF- setningen er en treveis aritmetisk betinget uttalelse, først sett i den første utgivelsen av Fortran i 1957, og ble funnet i alle senere versjoner, og noen andre programmeringsspråk, for eksempel FOCAL. I motsetning til de logiske IF-setningene sett på andre språk, definerer Fortran-setningen tre forskjellige grener, avhengig av om resultatet av et uttrykk er negativt, null eller positivt, i nevnte rekkefølge, skrevet som:
Aritmetisk hyperbolsk 3-manifold: I matematikk, nærmere bestemt i gruppeteori og hyperbolsk geometri, er aritmetiske Kleinian-grupper en spesiell klasse av Kleinian-grupper konstruert ved bruk av ordrer i kvaternionalgebraer. De er spesielle forekomster av aritmetiske grupper. En aritmetisk hyperbolsk tre-manifold er kvotienten til det hyperbolske rommet av en aritmetisk Kleinian-gruppe. Disse manifoldene inkluderer noen spesielt vakre eller bemerkelsesverdige eksempler.
Aritmetisk logikkenhet: I databehandling er en aritmetisk logisk enhet (ALU) en kombinasjons digital krets som utfører aritmetiske og bitvise operasjoner på heltall binære tall. Dette er i motsetning til en flytende punktenhet (FPU), som opererer på flytende nummer. Det er en grunnleggende byggestein for mange typer datakretser, inkludert den sentrale prosessorenheten (CPU) på datamaskiner, FPUer og grafikkbehandlingsenheter (GPUer).
Aritmetisk gjennomsnitt: I matematikk og statistikk er det aritmetiske gjennomsnittet , eller bare gjennomsnittet eller gjennomsnittet , summen av en samling av tall delt på antall tall i samlingen. Samlingen er ofte et sett med resultater fra et eksperiment eller en observasjonsstudie, eller ofte et sett med resultater fra en undersøkelse. Uttrykket "aritmetisk middel" foretrekkes i noen sammenhenger i matematikk og statistikk, fordi det hjelper å skille det fra andre måter, for eksempel det geometriske gjennomsnittet og det harmoniske gjennomsnittet.
Ulikhet mellom aritmetiske og geometriske betyr: I matematikk angir ulikheten mellom aritmetiske og geometriske midler , eller kort sagt AM – GM-ulikheten , at det aritmetiske gjennomsnittet av en liste over ikke-negative reelle tall er større enn eller lik det geometriske gjennomsnittet av den samme listen; og videre at de to midlene er like hvis og bare hvis hvert tall i listen er det samme.
Aritmetisk progresjon: En aritmetisk progresjon (AP) eller aritmetisk sekvens er en tallsekvens slik at forskjellen mellom de påfølgende ordene er konstant. For eksempel, sekvensen 5, 7, 9, 11, 13, 15 ,. .. er en aritmetisk progresjon med en felles forskjell på 2.
Arakelov teori: I matematikk er Arakelov-teorien en tilnærming til diofantinsk geometri, oppkalt etter Suren Arakelov. Den brukes til å studere diofantiske ligninger i høyere dimensjoner.
Arakelov teori: I matematikk er Arakelov-teorien en tilnærming til diofantinsk geometri, oppkalt etter Suren Arakelov. Den brukes til å studere diofantiske ligninger i høyere dimensjoner.
Aritmetisk progresjon: En aritmetisk progresjon (AP) eller aritmetisk sekvens er en tallsekvens slik at forskjellen mellom de påfølgende ordene er konstant. For eksempel, sekvensen 5, 7, 9, 11, 13, 15 ,. .. er en aritmetisk progresjon med en felles forskjell på 2.
Aritmetisk overflate: I matematikk, en aritmetisk overflate over et Dedekind-domene R med brøkfelt er et geometrisk objekt som har en konvensjonell dimensjon, og en annen dimensjon gitt av primtalens uendelige. Når R er ringen av heltall Z , avhenger denne intuisjonen av at det primære ideelle spekteret Spec ( Z ) blir sett på som analogt med en linje. Aritmetiske flater oppstår naturlig i diofantin geometri, når en algebraisk kurve definert over K antas å ha reduksjoner over feltene R / P , hvor P er et hovedideal for R , for nesten alle P ; og er nyttige i å spesifisere hva som skal skje med prosessen med å redusere til R / P når den mest naive måten ikke gir mening.
Algoritmisk handel: Algoritmisk handel er en metode for å utføre ordrer ved hjelp av automatiserte forhåndsprogrammerte handelsinstruksjoner som tar hensyn til variabler som tid, pris og volum. Denne typen handel prøver å utnytte hastigheten og beregningsressursene til datamaskiner i forhold til menneskelige handelsmenn. I det tjueførste århundre har algoritmisk handel fått grep med både detaljhandler og institusjonelle handelsmenn. Det brukes mye av investeringsbanker, pensjonsfond, verdipapirfond og hedgefond som kan trenge å spre utførelsen av en større ordre eller utføre handler for raskt for menneskelige handelsmenn å reagere på. En studie i 2019 viste at rundt 92% av handelen i Forex-markedet ble utført av handelsalgoritmer i stedet for mennesker.
Aritmetisk geometri: I matematikk er aritmetisk geometri omtrent anvendelse av teknikker fra algebraisk geometri til problemer i tallteori. Aritmetisk geometri er sentrert rundt Diophantine geometry, studiet av rasjonelle punkter av algebraiske varianter.
Aritmetisk logikkenhet: I databehandling er en aritmetisk logisk enhet (ALU) en kombinasjons digital krets som utfører aritmetiske og bitvise operasjoner på heltall binære tall. Dette er i motsetning til en flytende punktenhet (FPU), som opererer på flytende nummer. Det er en grunnleggende byggestein for mange typer datakretser, inkludert den sentrale prosessorenheten (CPU) på datamaskiner, FPUer og grafikkbehandlingsenheter (GPUer).
Regning og geometrisk Frobenius: I matematikk er Frobenius-endomorfismen definert i hvilken som helst kommutativ ring R som har karakteristisk p , hvor p er et primtall. Kartleggingen φ som tar r i R til r p er nemlig en ringendomorfisme av R.
Regning og geometrisk Frobenius: I matematikk er Frobenius-endomorfismen definert i hvilken som helst kommutativ ring R som har karakteristisk p , hvor p er et primtall. Kartleggingen φ som tar r i R til r p er nemlig en ringendomorfisme av R.
Instruksjonsarkitektur: I informatikk er en instruksjonsarkitektur ( ISA ) en abstrakt modell av en datamaskin. Det blir også referert til som arkitektur eller dataarkitektur . En realisering av en ISA, for eksempel en sentral prosesseringsenhet (CPU), kalles en implementering .
Aritmetisk logikkenhet: I databehandling er en aritmetisk logisk enhet (ALU) en kombinasjons digital krets som utfører aritmetiske og bitvise operasjoner på heltall binære tall. Dette er i motsetning til en flytende punktenhet (FPU), som opererer på flytende nummer. Det er en grunnleggende byggestein for mange typer datakretser, inkludert den sentrale prosessorenheten (CPU) på datamaskiner, FPUer og grafikkbehandlingsenheter (GPUer).
Aritmetisk logikkenhet: I databehandling er en aritmetisk logisk enhet (ALU) en kombinasjons digital krets som utfører aritmetiske og bitvise operasjoner på heltall binære tall. Dette er i motsetning til en flytende punktenhet (FPU), som opererer på flytende nummer. Det er en grunnleggende byggestein for mange typer datakretser, inkludert den sentrale prosessorenheten (CPU) på datamaskiner, FPUer og grafikkbehandlingsenheter (GPUer).
Aritmetisk logikkenhet: I databehandling er en aritmetisk logisk enhet (ALU) en kombinasjons digital krets som utfører aritmetiske og bitvise operasjoner på heltall binære tall. Dette er i motsetning til en flytende punktenhet (FPU), som opererer på flytende nummer. Det er en grunnleggende byggestein for mange typer datakretser, inkludert den sentrale prosessorenheten (CPU) på datamaskiner, FPUer og grafikkbehandlingsenheter (GPUer).
Gjennomsnitt: På språket er et gjennomsnitt et enkelt tall tatt som representativ for en ikke-tom liste. Ulike gjennomsnittlige begreper brukes i forskjellige sammenhenger. Ofte refererer "gjennomsnitt" til det aritmetiske gjennomsnittet, summen av tallene delt på hvor mange tall som blir gjennomsnittet. I statistikk er middel, median og modus alle kjent som mål for sentral tendens, og i daglig bruk kan noen av disse kalles en gjennomsnittsverdi .
Aritmetisk biljard: I rekreasjonsmatematikk gir aritmetiske biljard en geometrisk metode for å bestemme det minst vanlige multiplumet og den største fellesdeleren av to naturlige tall ved å bruke refleksjoner i et rektangel hvis sider er de to gitte tallene. Dette er et enkelt eksempel på baneanalyse av dynamisk biljard.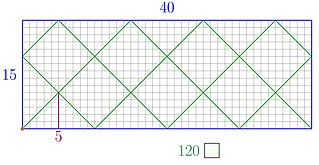
Aritmetisk krets kompleksitet: I teorien om beregningskompleksitet er aritmetiske kretser standardmodellen for beregning av polynomer. Uformelt tar en aritmetisk krets som innganger enten variabler eller tall, og har lov til å enten legge til eller multiplisere to uttrykk den allerede har beregnet. Aritmetiske kretser gir en formell måte å forstå kompleksiteten i databehandlingspolynomer. Den grunnleggende typen spørsmål i denne forskningen er "hva er den mest effektive måten å beregne et gitt polynom på ? "
Aritmetisk krets kompleksitet: I teorien om beregningskompleksitet er aritmetiske kretser standardmodellen for beregning av polynomer. Uformelt tar en aritmetisk krets som innganger enten variabler eller tall, og har lov til å enten legge til eller multiplisere to uttrykk den allerede har beregnet. Aritmetiske kretser gir en formell måte å forstå kompleksiteten i databehandlingspolynomer. Den grunnleggende typen spørsmål i denne forskningen er "hva er den mest effektive måten å beregne et gitt polynom på ? "
Aritmetisk krets kompleksitet: I teorien om beregningskompleksitet er aritmetiske kretser standardmodellen for beregning av polynomer. Uformelt tar en aritmetisk krets som innganger enten variabler eller tall, og har lov til å enten legge til eller multiplisere to uttrykk den allerede har beregnet. Aritmetiske kretser gir en formell måte å forstå kompleksiteten i databehandlingspolynomer. Den grunnleggende typen spørsmål i denne forskningen er "hva er den mest effektive måten å beregne et gitt polynom på ? "
Aritmetisk krets kompleksitet: I teorien om beregningskompleksitet er aritmetiske kretser standardmodellen for beregning av polynomer. Uformelt tar en aritmetisk krets som innganger enten variabler eller tall, og har lov til å enten legge til eller multiplisere to uttrykk den allerede har beregnet. Aritmetiske kretser gir en formell måte å forstå kompleksiteten i databehandlingspolynomer. Den grunnleggende typen spørsmål i denne forskningen er "hva er den mest effektive måten å beregne et gitt polynom på ? "
Aritmetisk koding: Aritmetisk koding ( AC ) er en form for entropikoding som brukes i tapsfri datakomprimering. Normalt blir en streng med tegn som ordene "hallo der" representert ved hjelp av et fast antall bits per tegn, som i ASCII-koden. Når en streng konverteres til aritmetisk koding, lagres ofte brukte tegn med færre biter, og ikke så ofte forekommende tegn lagres med flere biter, noe som resulterer i færre biter som brukes totalt. Aritmetisk koding skiller seg fra andre former for entropikoding, for eksempel Huffman-koding, ved at i stedet for å skille inngangen i komponentsymboler og erstatte hver med en kode, koder aritmetisk koding hele meldingen til et enkelt tall, en vilkårlig presisjonsfraksjon q , hvor 0,0 ≤ q <1,0 . Den representerer gjeldende informasjon som et område, definert av to tall. En nylig familie av entropikodere kalt asymmetriske tallsystemer muliggjør raskere implementeringer takket være direkte drift på et enkelt naturlig tall som representerer gjeldende informasjon.
Aritmetisk koding: Aritmetisk koding ( AC ) er en form for entropikoding som brukes i tapsfri datakomprimering. Normalt blir en streng med tegn som ordene "hallo der" representert ved hjelp av et fast antall bits per tegn, som i ASCII-koden. Når en streng konverteres til aritmetisk koding, lagres ofte brukte tegn med færre biter, og ikke så ofte forekommende tegn lagres med flere biter, noe som resulterer i færre biter som brukes totalt. Aritmetisk koding skiller seg fra andre former for entropikoding, for eksempel Huffman-koding, ved at i stedet for å skille inngangen i komponentsymboler og erstatte hver med en kode, koder aritmetisk koding hele meldingen til et enkelt tall, en vilkårlig presisjonsfraksjon q , hvor 0,0 ≤ q <1,0 . Den representerer gjeldende informasjon som et område, definert av to tall. En nylig familie av entropikodere kalt asymmetriske tallsystemer muliggjør raskere implementeringer takket være direkte drift på et enkelt naturlig tall som representerer gjeldende informasjon.
Aritmetisk koding: Aritmetisk koding ( AC ) er en form for entropikoding som brukes i tapsfri datakomprimering. Normalt blir en streng med tegn som ordene "hallo der" representert ved hjelp av et fast antall bits per tegn, som i ASCII-koden. Når en streng konverteres til aritmetisk koding, lagres ofte brukte tegn med færre biter, og ikke så ofte forekommende tegn lagres med flere biter, noe som resulterer i færre biter som brukes totalt. Aritmetisk koding skiller seg fra andre former for entropikoding, for eksempel Huffman-koding, ved at i stedet for å skille inngangen i komponentsymboler og erstatte hver med en kode, koder aritmetisk koding hele meldingen til et enkelt tall, en vilkårlig presisjonsfraksjon q , hvor 0,0 ≤ q <1,0 . Den representerer gjeldende informasjon som et område, definert av to tall. En nylig familie av entropikodere kalt asymmetriske tallsystemer muliggjør raskere implementeringer takket være direkte drift på et enkelt naturlig tall som representerer gjeldende informasjon.
Aritmetisk kombinatorikk: I matematikk er aritmetisk kombinatorikk et felt i skjæringspunktet mellom tallteori, kombinatorikk, ergodisk teori og harmonisk analyse.
Rask Fourier-transformasjon: En rask Fourier-transformasjon ( FFT ) er en algoritme som beregner den diskrete Fourier-transformasjonen (DFT) til en sekvens, eller dens inverse (IDFT). Fourier-analyse konverterer et signal fra sitt opprinnelige domene til en representasjon i frekvensdomenet og omvendt. DFT oppnås ved å spalte en sekvens av verdier til komponenter med forskjellige frekvenser. Denne operasjonen er nyttig på mange felt, men å beregne den direkte fra definisjonen er ofte for treg til å være praktisk. En FFT beregner raskt slike transformasjoner ved å faktorisere DFT-matrisen til et produkt av sparsomme faktorer. Som et resultat klarer den å redusere kompleksiteten ved å beregne DFT fra , som oppstår hvis man bare bruker definisjonen av DFT, til , hvor er datastørrelsen. Forskjellen i hastighet kan være enorm, spesielt for lange datasett der N kan være tusenvis eller millioner. I nærvær av avrundingsfeil er mange FFT-algoritmer mye mer nøyaktige enn å evaluere DFT-definisjonen direkte eller indirekte. Det er mange forskjellige FFT-algoritmer basert på et bredt spekter av publiserte teorier, fra enkel aritmetikk med komplekse tall til gruppeteori og tallteori.
Rask Fourier-transformasjon: En rask Fourier-transformasjon ( FFT ) er en algoritme som beregner den diskrete Fourier-transformasjonen (DFT) til en sekvens, eller dens inverse (IDFT). Fourier-analyse konverterer et signal fra sitt opprinnelige domene til en representasjon i frekvensdomenet og omvendt. DFT oppnås ved å spalte en sekvens av verdier til komponenter med forskjellige frekvenser. Denne operasjonen er nyttig på mange felt, men å beregne den direkte fra definisjonen er ofte for treg til å være praktisk. En FFT beregner raskt slike transformasjoner ved å faktorisere DFT-matrisen til et produkt av sparsomme faktorer. Som et resultat klarer den å redusere kompleksiteten ved å beregne DFT fra , som oppstår hvis man bare bruker definisjonen av DFT, til , hvor er datastørrelsen. Forskjellen i hastighet kan være enorm, spesielt for lange datasett der N kan være tusenvis eller millioner. I nærvær av avrundingsfeil er mange FFT-algoritmer mye mer nøyaktige enn å evaluere DFT-definisjonen direkte eller indirekte. Det er mange forskjellige FFT-algoritmer basert på et bredt spekter av publiserte teorier, fra enkel aritmetikk med komplekse tall til gruppeteori og tallteori.
Interuniversal Teichmüller-teori: Interuniversal Teichmüller-teori er navnet som matematikeren Shinichi Mochizuki ga til en teori han utviklet på 2000-tallet, etter hans tidligere arbeid i aritmetisk geometri. Ifølge Mochizuki er det "en aritmetisk versjon av Teichmüller-teorien for tallfelt utstyrt med en elliptisk kurve". Teorien ble offentliggjort i en serie med fire fortrykk som ble lagt ut i 2012 på nettstedet hans. Den mest slående påståtte anvendelsen av teorien er å gi et bevis for forskjellige fremragende antagelser innen tallteori, spesielt abc- antagelsen . Mochizuki og noen få andre matematikere hevder at teorien virkelig gir et slikt bevis, men dette har hittil ikke blitt akseptert av det matematiske samfunnet.
Naturlig tetthet: I tallteori er naturlig tetthet en metode for å måle hvor "stor" en delmengde av settet med naturlige tall er. Den er hovedsakelig avhengig av sannsynligheten for å møte medlemmer av ønsket delmengde når du kammer gjennom intervallet [1, n ] når n blir stor.
Aritmetiske derivater: I tallteori, den Lagarias aritmetiske derivat, eller et tall derivat, er en funksjon definert for hele tall, basert på Primtallfaktorisering, ved analogi med produktet regelen for den deriverte av en funksjon som brukes i matematisk analyse.
Aritmetisk dynamikk: Aritmetisk dynamikk er et felt som samler to områder innen matematikk, dynamiske systemer og tallteori. Klassisk refererer diskret dynamikk til studien av iterasjonen av selvkart over det komplekse planet eller den virkelige linjen. Aritmetisk dynamikk er studiet av tallteoretiske egenskaper til heltall, rasjonelle, p -adiske og / eller algebraiske punkter under gjentatt anvendelse av en polynom eller rasjonell funksjon. Et grunnleggende mål er å beskrive aritmetiske egenskaper i form av underliggende geometriske strukturer.
Aritmetisk koding: Aritmetisk koding ( AC ) er en form for entropikoding som brukes i tapsfri datakomprimering. Normalt blir en streng med tegn som ordene "hallo der" representert ved hjelp av et fast antall bits per tegn, som i ASCII-koden. Når en streng konverteres til aritmetisk koding, lagres ofte brukte tegn med færre biter, og ikke så ofte forekommende tegn lagres med flere biter, noe som resulterer i færre biter som brukes totalt. Aritmetisk koding skiller seg fra andre former for entropikoding, for eksempel Huffman-koding, ved at i stedet for å skille inngangen i komponentsymboler og erstatte hver med en kode, koder aritmetisk koding hele meldingen til et enkelt tall, en vilkårlig presisjonsfraksjon q , hvor 0,0 ≤ q <1,0 . Den representerer gjeldende informasjon som et område, definert av to tall. En nylig familie av entropikodere kalt asymmetriske tallsystemer muliggjør raskere implementeringer takket være direkte drift på et enkelt naturlig tall som representerer gjeldende informasjon.
Aritmetisk koding: Aritmetisk koding ( AC ) er en form for entropikoding som brukes i tapsfri datakomprimering. Normalt blir en streng med tegn som ordene "hallo der" representert ved hjelp av et fast antall bits per tegn, som i ASCII-koden. Når en streng konverteres til aritmetisk koding, lagres ofte brukte tegn med færre biter, og ikke så ofte forekommende tegn lagres med flere biter, noe som resulterer i færre biter som brukes totalt. Aritmetisk koding skiller seg fra andre former for entropikoding, for eksempel Huffman-koding, ved at i stedet for å skille inngangen i komponentsymboler og erstatte hver med en kode, koder aritmetisk koding hele meldingen til et enkelt tall, en vilkårlig presisjonsfraksjon q , hvor 0,0 ≤ q <1,0 . Den representerer gjeldende informasjon som et område, definert av to tall. En nylig familie av entropikodere kalt asymmetriske tallsystemer muliggjør raskere implementeringer takket være direkte drift på et enkelt naturlig tall som representerer gjeldende informasjon.
Uttrykk (matematikk): I matematikk er et uttrykk eller et matematisk uttrykk en endelig kombinasjon av symboler som er godt formet etter regler som avhenger av sammenhengen. Matematiske symboler kan betegne tall (konstanter), variabler, operasjoner, funksjoner, parenteser, tegnsetting og gruppering for å bestemme rekkefølgen av operasjoner og andre aspekter av logisk syntaks.
Regning for foreldre: Arithmetic for Parents er en bok om matematikkopplæring rettet mot foreldre og lærere.
Regning for foreldre: Arithmetic for Parents er en bok om matematikkopplæring rettet mot foreldre og lærere.
Peano-aksiomer: I matematisk logikk er Peano-aksiomene , også kjent som Dedekind – Peano-aksiomer eller Peano-postulater , aksiomer for de naturlige tallene som ble presentert av det italienske matematikeren Giuseppe Peano fra 1800-tallet. Disse aksiomene har blitt brukt nesten uendret i en rekke metamatiske undersøkelser, inkludert forskning i grunnleggende spørsmål om tallteori er konsistent og komplett.
Brøkdel: En brøkdel representerer en del av en helhet, eller mer generelt, et hvilket som helst antall like deler. Når det snakkes på hverdagsengelsk, beskriver en brøkdel hvor mange deler av en viss størrelse det er, for eksempel halvparten, åtte femtedeler og tre fjerdedeler. En vanlig , vulgær eller enkel brøkdel består av en teller som vises over en linje, og en ikke-null- nevner , vist under den linjen. Teller og nevner benyttes også i fraksjoner som ikke er vanlige , inkludert sammensatte fraksjoner, komplekse fraksjoner og blandede tall.
Aritmetisk funksjon: I tallteori er en aritmetisk , aritmetisk eller tallteoretisk funksjon for de fleste forfattere enhver funksjon f ( n ) hvis domene er de positive heltallene og hvis område er en delmengde av de komplekse tallene. Hardy & Wright inkluderer i sin definisjon kravet om at en aritmetisk funksjon "uttrykker noen aritmetiske egenskaper til n ".
Aritmetisk funksjon: I tallteori er en aritmetisk , aritmetisk eller tallteoretisk funksjon for de fleste forfattere enhver funksjon f ( n ) hvis domene er de positive heltallene og hvis område er en delmengde av de komplekse tallene. Hardy & Wright inkluderer i sin definisjon kravet om at en aritmetisk funksjon "uttrykker noen aritmetiske egenskaper til n ".
Aritmetisk slekt: I matematikk er den aritmetiske slekten til en algebraisk variant en av få mulige generaliseringer av slekten til en algebraisk kurve eller Riemann-overflate.
Aritmetisk – geometrisk gjennomsnitt: I matematikk er det aritmetiske-geometriske gjennomsnittet ( AGM ) av to positive reelle tall x og y definert som følger:
Aritmetisk geometri: I matematikk er aritmetisk geometri omtrent anvendelse av teknikker fra algebraisk geometri til problemer i tallteori. Aritmetisk geometri er sentrert rundt Diophantine geometry, studiet av rasjonelle punkter av algebraiske varianter.
Aritmetisk gruppe: I matematikk er en aritmetisk gruppe en gruppe oppnådd som heltallene til en algebraisk gruppe, for eksempel De oppstår naturlig i studiet av aritmetiske egenskaper til kvadratiske former og andre klassiske emner i tallteori. De gir også opphav til veldig interessante eksempler på Riemannian manifolds og er derfor objekter av interesse for differensial geometri og topologi. Til slutt blir disse to emnene med i teorien om automatiske former som er grunnleggende i moderne tallteori.
Lineær funksjon: I matematikk refererer begrepet lineær funksjon til to forskjellige, men beslektede forestillinger: I kalkulator og relaterte områder er en lineær funksjon en funksjon hvis graf er en rett linje, det vil si en polynomfunksjon av grad null eller en. For å skille en slik lineær funksjon fra det andre konseptet, brukes ofte begrepet affin funksjon. I lineær algebra, matematisk analyse og funksjonell analyse er en lineær funksjon et lineært kart.
Geometrisk gjennomsnitt: I matematikk er det geometriske gjennomsnittet et gjennomsnitt eller gjennomsnitt, som indikerer den sentrale tendensen eller den typiske verdien til et sett med tall ved å bruke produktet av deres verdier. Den geometriske middelverdi er definert som den n-te rot av produktet av n antall, det vil si, for et sett med tall x 1, X2, ..., Xn, det geometriske gjennomsnittet er definert som
Aritmetisk hierarki: I matematisk logikk klassifiserer det aritmetiske hierarkiet , det aritmetiske hierarkiet eller Kleene – Mostowski-hierarkiet visse sett basert på kompleksiteten i formler som definerer dem. Ethvert sett som mottar en klassifisering kalles aritmetisk .
Aritmetisk hyperbolsk 3-manifold: I matematikk, nærmere bestemt i gruppeteori og hyperbolsk geometri, er aritmetiske Kleinian-grupper en spesiell klasse av Kleinian-grupper konstruert ved bruk av ordrer i kvaternionalgebraer. De er spesielle forekomster av aritmetiske grupper. En aritmetisk hyperbolsk tre-manifold er kvotienten til det hyperbolske rommet av en aritmetisk Kleinian-gruppe. Disse manifoldene inkluderer noen spesielt vakre eller bemerkelsesverdige eksempler.
Aritmetisk fuchsisk gruppe: Aritmetiske fuchsiske grupper er en spesiell klasse av fuchsiske grupper konstruert ved bruk av ordrer i kvaternionsalgebras. De er spesielle forekomster av aritmetiske grupper. Det prototypiske eksemplet på en aritmetisk Fuchsian-gruppe er modulgruppen . De og den hyperbolske overflaten assosiert med deres virkning på det hyperbolske planet viser ofte spesielt regelmessig oppførsel blant fuchsiske grupper og hyperbolske overflater.
Aritmetikk IF: Den aritmetiske IF- setningen er en treveis aritmetisk betinget uttalelse, først sett i den første utgivelsen av Fortran i 1957, og ble funnet i alle senere versjoner, og noen andre programmeringsspråk, for eksempel FOCAL. I motsetning til de logiske IF-setningene sett på andre språk, definerer Fortran-setningen tre forskjellige grener, avhengig av om resultatet av et uttrykk er negativt, null eller positivt, i nevnte rekkefølge, skrevet som:
De ni kapitlene om matematisk kunst: De ni kapitlene om matematisk kunst er en kinesisk matematikkbok, komponert av flere generasjoner forskere fra det 10. – 2. århundre f.Kr., og den siste fasen er fra det 2. århundre. Denne boka er en av de tidligste gjenlevende matematiske tekstene fra Kina, den første er Suan shu shu og Zhoubi Suanjing . Den legger opp til en tilnærming til matematikk som fokuserer på å finne de mest generelle metodene for å løse problemer, noe som kan være i motsetning til den tilnærmingen som er vanlig for gamle greske matematikere, som hadde en tendens til å utlede proposisjoner fra et første sett med aksiomer.
Endelig feltaritmetikk: I matematikk er endelig feltaritmetikk aritmetikk i et endelig felt i motsetning til aritmetikk i et felt med et uendelig antall elementer, som feltet rasjonelle tall.
De ni kapitlene om matematisk kunst: De ni kapitlene om matematisk kunst er en kinesisk matematikkbok, komponert av flere generasjoner forskere fra det 10. – 2. århundre f.Kr., og den siste fasen er fra det 2. århundre. Denne boka er en av de tidligste gjenlevende matematiske tekstene fra Kina, den første er Suan shu shu og Zhoubi Suanjing . Den legger opp til en tilnærming til matematikk som fokuserer på å finne de mest generelle metodene for å løse problemer, noe som kan være i motsetning til den tilnærmingen som er vanlig for gamle greske matematikere, som hadde en tendens til å utlede proposisjoner fra et første sett med aksiomer.
Takmodell: Roofline-modellen er en intuitiv visuell ytelsesmodell som brukes til å gi ytelsesestimater for en gitt beregningskjerne eller applikasjon som kjører på flerkjernede, mangekjernede eller akseleratorprosessorarkitekturer, ved å vise iboende maskinvarebegrensninger, og potensiell fordel og prioritet ved optimaliseringer. Ved å kombinere lokalitet, båndbredde og forskjellige parallelliseringsparadigmer i en enkelt ytelsesfigur, kan modellen være et effektivt alternativ for å vurdere kvaliteten på oppnådd ytelse i stedet for å bruke enkle prosent-av-toppestimater, da den gir innsikt i både implementeringen og iboende ytelsesbegrensninger.
Multiplikativ invers: I matematikk er en multiplikativ invers eller gjensidig for et tall x , betegnet med 1 / x eller x −1 , et tall som når multiplisert med x gir den multipliserende identiteten, 1. Multiplikasjonsinversen av en brøk a / b er b / a . For multiplikativ invers av et reelt tall, divider 1 med tallet. For eksempel er den gjensidige på 5 en femtedel, og den gjensidige på 0,25 er 1 delt på 0,25 eller 4. Den gjensidige funksjonen , funksjonen f ( x ) som kartlegger x til 1 / x , er et av de enkleste eksemplene på en funksjon som er dens egen invers.
Gitter (diskret undergruppe): I Lie-teorien og relaterte matematikkområder er et gitter i en lokalt kompakt gruppe en diskret undergruppe med den egenskapen at kvotientrommet har endelig invariant mål. I det spesielle tilfelle av undergrupper av R, n, utgjør dette den vanlige geometriske oppfatningen av et gitter som en periodisk delmengde av punkter, og både den algebraiske strukturen av gittere og geometrien til den plass av alle gittere er relativt godt forstått.
Dyskalculia: Dyskalculia er en funksjonshemning som resulterer i vanskeligheter med å lære eller forstå aritmetikk, for eksempel vanskeligheter med å forstå tall, lære å manipulere tall, utføre matematiske beregninger og lære fakta i matematikk. Det er noen ganger uformelt kjent som "matematisk dysleksi", selv om dette kan være misvisende, ettersom dysleksi er en annen tilstand enn dyscalculia.
Aritmetisk skift: I dataprogrammering er et aritmetisk skift en skiftoperatør, noen ganger kalt et signert skift . De to grunnleggende typene er det aritmetiske venstre skiftet og det aritmetiske høyre skiftet . For binære tall er det en bitvis operasjon som forskyver alle bitene i operanden; hver bit i operanden flyttes ganske enkelt et gitt antall bitposisjoner, og de ledige bitposisjonene fylles ut. I stedet for å bli fylt med alle 0s, som i logisk skift, blir den venstre biten replikert til høyre fyll i alle ledige stillinger.
Aritmetisk logikkenhet: I databehandling er en aritmetisk logisk enhet (ALU) en kombinasjons digital krets som utfører aritmetiske og bitvise operasjoner på heltall binære tall. Dette er i motsetning til en flytende punktenhet (FPU), som opererer på flytende nummer. Det er en grunnleggende byggestein for mange typer datakretser, inkludert den sentrale prosessorenheten (CPU) på datamaskiner, FPUer og grafikkbehandlingsenheter (GPUer).
Aritmetisk logikkenhet: I databehandling er en aritmetisk logisk enhet (ALU) en kombinasjons digital krets som utfører aritmetiske og bitvise operasjoner på heltall binære tall. Dette er i motsetning til en flytende punktenhet (FPU), som opererer på flytende nummer. Det er en grunnleggende byggestein for mange typer datakretser, inkludert den sentrale prosessorenheten (CPU) på datamaskiner, FPUer og grafikkbehandlingsenheter (GPUer).
Aritmetisk logikkenhet: I databehandling er en aritmetisk logisk enhet (ALU) en kombinasjons digital krets som utfører aritmetiske og bitvise operasjoner på heltall binære tall. Dette er i motsetning til en flytende punktenhet (FPU), som opererer på flytende nummer. Det er en grunnleggende byggestein for mange typer datakretser, inkludert den sentrale prosessorenheten (CPU) på datamaskiner, FPUer og grafikkbehandlingsenheter (GPUer).
Pascals kalkulator: Pascals kalkulator er en mekanisk kalkulator som ble oppfunnet av Blaise Pascal på midten av 1600-tallet. Pascal ble ledet til å utvikle en kalkulator ved de møysommelige aritmetiske beregningene som kreves av farens arbeid som skattetilsyn i Rouen. Han designet maskinen for å legge til og trekke fra to tall direkte, og for å utføre multiplikasjon og deling gjennom gjentatt addisjon eller subtraksjon.
Aritmetisk gjennomsnitt: I matematikk og statistikk er det aritmetiske gjennomsnittet , eller bare gjennomsnittet eller gjennomsnittet , summen av en samling av tall delt på antall tall i samlingen. Samlingen er ofte et sett med resultater fra et eksperiment eller en observasjonsstudie, eller ofte et sett med resultater fra en undersøkelse. Uttrykket "aritmetisk middel" foretrekkes i noen sammenhenger i matematikk og statistikk, fordi det hjelper å skille det fra andre måter, for eksempel det geometriske gjennomsnittet og det harmoniske gjennomsnittet.
Ulikhet mellom aritmetiske og geometriske betyr: I matematikk angir ulikheten mellom aritmetiske og geometriske midler , eller kort sagt AM – GM-ulikheten , at det aritmetiske gjennomsnittet av en liste over ikke-negative reelle tall er større enn eller lik det geometriske gjennomsnittet av den samme listen; og videre at de to midlene er like hvis og bare hvis hvert tall i listen er det samme.
Norm (matematikk): I matematikk er en norm en funksjon fra et reelt eller komplekst vektorrom til de ikke-negative reelle tallene som oppfører seg på bestemte måter som avstanden fra opprinnelsen: den pendler med skalering, adlyder en form for trekant-ulikhet og er null bare ved Opprinnelsen. Spesielt er den euklidiske avstanden til en vektor fra opprinnelsen en norm, kalt den euklidiske normen, eller 2-norm, som også kan defineres som kvadratroten av det indre produktet av en vektor med seg selv.
Aritmetisk nummer: I tallteori er et aritmetisk tall et heltall der gjennomsnittet av dets positive delere også er et helt tall. For eksempel er 6 et aritmetisk tall fordi gjennomsnittet av delene er
Aritmetikk av et drap: Arithmetic of a Murder er en sovjetisk kriminalfilm fra 1991 regissert av Dmitry Svetozarov.
Aritmetikk av abelske varianter: I matematikk er aritmetikken til abelske varianter studiet av tallteorien til en abelsvariant, eller en familie av abelske varianter. Det går tilbake til studiene av Pierre de Fermat på det som nå er anerkjent som elliptiske kurver; og har blitt et veldig betydelig område av aritmetisk geometri både når det gjelder resultater og antagelser. De fleste av disse kan stilles for en abelsk variant A over et tallfelt K ; eller mer generelt.
Aritmetikk av abelske varianter: I matematikk er aritmetikken til abelske varianter studiet av tallteorien til en abelsvariant, eller en familie av abelske varianter. Det går tilbake til studiene av Pierre de Fermat på det som nå er anerkjent som elliptiske kurver; og har blitt et veldig betydelig område av aritmetisk geometri både når det gjelder resultater og antagelser. De fleste av disse kan stilles for en abelsk variant A over et tallfelt K ; eller mer generelt.
Aritmetikk av abelske varianter: I matematikk er aritmetikken til abelske varianter studiet av tallteorien til en abelsvariant, eller en familie av abelske varianter. Det går tilbake til studiene av Pierre de Fermat på det som nå er anerkjent som elliptiske kurver; og har blitt et veldig betydelig område av aritmetisk geometri både når det gjelder resultater og antagelser. De fleste av disse kan stilles for en abelsk variant A over et tallfelt K ; eller mer generelt.
Endelig feltaritmetikk: I matematikk er endelig feltaritmetikk aritmetikk i et endelig felt i motsetning til aritmetikk i et felt med et uendelig antall elementer, som feltet rasjonelle tall.
Ordinær aritmetikk: I det matematiske feltet med mengdeteori beskriver ordinær aritmetikk de tre vanlige operasjonene på ordinale tall: addisjon, multiplikasjon og eksponentiering. Hver kan defineres på to forskjellige måter: enten ved å konstruere et eksplisitt velordnet sett som representerer operasjonen eller ved å bruke transfinite rekursjon. Cantor normalform gir en standardisert måte å skrive ordinals på. I tillegg til disse vanlige ordinale operasjonene, er det også den "naturlige" aritmetikken til ordinals og nimberoperasjonene.
Aritmetikk: Aritmetikk er en gren av matematikk som består av studiet av tall, spesielt egenskapene til de tradisjonelle operasjonene på dem — addisjon, subtraksjon, multiplikasjon, divisjon, eksponentiering og ekstraksjon av røtter. Aritmetikk er en elementær del av tallteori, og tallteori anses å være en av de øverste nivåene i moderne matematikk, sammen med algebra, geometri og analyse. Begrepene aritmetikk og høyere aritmetikk ble brukt til begynnelsen av 1900-tallet som synonymer for tallteori , og brukes noen ganger fortsatt til å referere til en bredere del av tallteorien.
Aritmetikk: Aritmetikk er en gren av matematikk som består av studiet av tall, spesielt egenskapene til de tradisjonelle operasjonene på dem — addisjon, subtraksjon, multiplikasjon, divisjon, eksponentiering og ekstraksjon av røtter. Aritmetikk er en elementær del av tallteori, og tallteori anses å være en av de øverste nivåene i moderne matematikk, sammen med algebra, geometri og analyse. Begrepene aritmetikk og høyere aritmetikk ble brukt til begynnelsen av 1900-tallet som synonymer for tallteori , og brukes noen ganger fortsatt til å referere til en bredere del av tallteorien.
Aritmetikk: Aritmetikk er en gren av matematikk som består av studiet av tall, spesielt egenskapene til de tradisjonelle operasjonene på dem — addisjon, subtraksjon, multiplikasjon, divisjon, eksponentiering og ekstraksjon av røtter. Aritmetikk er en elementær del av tallteori, og tallteori anses å være en av de øverste nivåene i moderne matematikk, sammen med algebra, geometri og analyse. Begrepene aritmetikk og høyere aritmetikk ble brukt til begynnelsen av 1900-tallet som synonymer for tallteori , og brukes noen ganger fortsatt til å referere til en bredere del av tallteorien.
Aritmetikk: Aritmetikk er en gren av matematikk som består av studiet av tall, spesielt egenskapene til de tradisjonelle operasjonene på dem — addisjon, subtraksjon, multiplikasjon, divisjon, eksponentiering og ekstraksjon av røtter. Aritmetikk er en elementær del av tallteori, og tallteori anses å være en av de øverste nivåene i moderne matematikk, sammen med algebra, geometri og analyse. Begrepene aritmetikk og høyere aritmetikk ble brukt til begynnelsen av 1900-tallet som synonymer for tallteori , og brukes noen ganger fortsatt til å referere til en bredere del av tallteorien.
Heltalloverløp: I programmering, oppstår det en heltalloverflyt når en aritmetisk operasjon forsøk på å skape en numerisk verdi som ligger utenfor det område som kan representeres med et gitt antall sifre - enten høyere enn den maksimale eller lavere enn den minimumsverdi representeres.
P-adic L-funksjon: I matematikk er en p -adisk zeta-funksjon , eller mer generelt en p -adic L- funksjon , en funksjon som er analog med Riemann-zeta-funksjonen, eller mer generelle L- funksjoner , men hvis domene og mål er p-adic . For eksempel, kan domenet være p -adic heltall Z p, en profinite p -gruppe, eller en p -adic familie av Galois representasjoner, og bildet kan være p -adic tall Q p eller den algebraiske lukking.
Viktige tall: Vesentlige tall på et tall i posisjonsnotasjon er sifre i tallet som er pålitelige og helt nødvendige for å indikere mengden av noe. Hvis et tall som uttrykker resultatet av måling av noe, har flere sifre enn sifrene som er tillatt av måleoppløsningen, er bare sifrene som er tillatt av måleoppløsningen pålitelige, så bare dette kan være viktige tall. For eksempel, hvis en lengdemåling gir 114,8 mm mens det minste intervallet mellom merkene på linjalen som brukes i målingen er 1 mm, så er de tre første sifrene bare pålitelige, så det kan være betydelige tall. Blant disse sifrene er det usikkerhet i det siste sifferet, men det regnes også som en betydelig figur siden sifre som er usikre, men pålitelige , betraktes som betydelige tall. Et annet eksempel er en volummåling på 2,98 L med usikkerheten på ± 0,05 L. Det faktiske volumet er et sted mellom 2,93 L og 3,03 L. Selv om alle tre sifrene ikke er sikre, men pålitelige, da disse indikerer det faktiske volumet med akseptabel usikkerhet . Så dette er viktige tall.
Aritmetisk progresjon: En aritmetisk progresjon (AP) eller aritmetisk sekvens er en tallsekvens slik at forskjellen mellom de påfølgende ordene er konstant. For eksempel, sekvensen 5, 7, 9, 11, 13, 15 ,. .. er en aritmetisk progresjon med en felles forskjell på 2.
Aritmetisk progresjonsspill: Det aritmetiske progresjonsspillet er et posisjonsspill der to spillere vekselvis velger tall, og prøver å oppta en komplett aritmetisk progresjon av en gitt størrelse.
Aritmetisk progresjon: En aritmetisk progresjon (AP) eller aritmetisk sekvens er en tallsekvens slik at forskjellen mellom de påfølgende ordene er konstant. For eksempel, sekvensen 5, 7, 9, 11, 13, 15 ,. .. er en aritmetisk progresjon med en felles forskjell på 2.
Ring (matematikk): I matematikk er ringer algebraiske strukturer som generaliserer felt: multiplikasjon trenger ikke være kommutativ og multiplikative inverser trenger ikke eksistere. Med andre ord er en ring et sett utstyrt med to binære operasjoner som tilfredsstiller egenskaper som er analoge med addisjon og multiplikasjon av heltall. Ringelementer kan være tall som heltall eller komplekse tall, men de kan også være ikke-numeriske objekter som polynomer, firkantede matriser, funksjoner og kraftserier.
Aritmetisk hierarki: I matematisk logikk klassifiserer det aritmetiske hierarkiet , det aritmetiske hierarkiet eller Kleene – Mostowski-hierarkiet visse sett basert på kompleksiteten i formler som definerer dem. Ethvert sett som mottar en klassifisering kalles aritmetisk .
Avkastning: I finans er avkastning et overskudd på en investering. Den omfatter enhver verdiendring på investeringen og / eller kontantstrømmer som investoren mottar fra den investeringen, for eksempel rentebetalinger, kuponger, kontantutbytte, aksjeutbytte eller utbetaling fra et derivat eller strukturert produkt. Det kan måles enten i absolutte termer eller i prosent av investerte beløp. Sistnevnte kalles også avkastningsperioden.
Aritmetisk skift: I dataprogrammering er et aritmetisk skift en skiftoperatør, noen ganger kalt et signert skift . De to grunnleggende typene er det aritmetiske venstre skiftet og det aritmetiske høyre skiftet . For binære tall er det en bitvis operasjon som forskyver alle bitene i operanden; hver bit i operanden flyttes ganske enkelt et gitt antall bitposisjoner, og de ledige bitposisjonene fylles ut. I stedet for å bli fylt med alle 0s, som i logisk skift, blir den venstre biten replikert til høyre fyll i alle ledige stillinger.
Aritmetisk ring: I algebra sies det at en kommutativ ring R er aritmetisk hvis noen av følgende ekvivalente forhold holder: Lokaliseringen av R kl er en uniserial ring for hvert maksimale ideal av R. For alle idealer , og , For alle idealer , og ,
Aritmetisk tau: Det aritmetiske tauet , eller det knyttede tauet , var et mye brukt aritmetisk verktøy i middelalderen som kunne brukes til å løse mange matematiske og geometriske problemer.
Arakelov teori: I matematikk er Arakelov-teorien en tilnærming til diofantinsk geometri, oppkalt etter Suren Arakelov. Den brukes til å studere diofantiske ligninger i høyere dimensjoner.
Abstrakt analytisk tallteori: Abstrakt analytisk tallteori er en gren av matematikk som tar ideene og teknikkene til klassisk analytisk tallteori og bruker dem på en rekke forskjellige matematiske felt. Det klassiske primtallsetningen fungerer som et prototypisk eksempel, og vekten er på abstrakte asymptotiske fordelingsresultater. Teorien ble oppfunnet og utviklet av matematikere som John Knopfmacher og Arne Beurling i det tjuende århundre.
Aritmetisk progresjon: En aritmetisk progresjon (AP) eller aritmetisk sekvens er en tallsekvens slik at forskjellen mellom de påfølgende ordene er konstant. For eksempel, sekvensen 5, 7, 9, 11, 13, 15 ,. .. er en aritmetisk progresjon med en felles forskjell på 2.
Aritmetisk progresjon: En aritmetisk progresjon (AP) eller aritmetisk sekvens er en tallsekvens slik at forskjellen mellom de påfølgende ordene er konstant. For eksempel, sekvensen 5, 7, 9, 11, 13, 15 ,. .. er en aritmetisk progresjon med en felles forskjell på 2.
Aritmetisk sett: I matematisk logikk er et aritmetisk sett et sett med naturlige tall som kan defineres med en formel av førsteordens Peano-aritmetikk. De aritmetiske settene er klassifisert etter det aritmetiske hierarkiet.
Aritmetisk skift: I dataprogrammering er et aritmetisk skift en skiftoperatør, noen ganger kalt et signert skift . De to grunnleggende typene er det aritmetiske venstre skiftet og det aritmetiske høyre skiftet . For binære tall er det en bitvis operasjon som forskyver alle bitene i operanden; hver bit i operanden flyttes ganske enkelt et gitt antall bitposisjoner, og de ledige bitposisjonene fylles ut. I stedet for å bli fylt med alle 0s, som i logisk skift, blir den venstre biten replikert til høyre fyll i alle ledige stillinger.
Psykisk beregning: Mental beregning består av aritmetiske beregninger som bare bruker den menneskelige hjerne, uten hjelp fra forsyninger eller enheter, for eksempel en kalkulator. Folk bruker mental beregning når databehandlingsverktøy ikke er tilgjengelige, når det er raskere enn andre beregningsmetoder, eller til og med i konkurransesammenheng. Mental beregning innebærer ofte bruk av spesifikke teknikker utviklet for spesifikke typer problemer. Personer med uvanlig høy evne til å utføre mentale beregninger kalles mentale kalkulatorer eller lynkalkulatorer .
Psykisk beregning: Mental beregning består av aritmetiske beregninger som bare bruker den menneskelige hjerne, uten hjelp fra forsyninger eller enheter, for eksempel en kalkulator. Folk bruker mental beregning når databehandlingsverktøy ikke er tilgjengelige, når det er raskere enn andre beregningsmetoder, eller til og med i konkurransesammenheng. Mental beregning innebærer ofte bruk av spesifikke teknikker utviklet for spesifikke typer problemer. Personer med uvanlig høy evne til å utføre mentale beregninger kalles mentale kalkulatorer eller lynkalkulatorer .
Sunnhet: I logikk, mer presist i deduktiv resonnement, er et argument forsvarlig hvis det både er gyldig i form og dets premisser er sanne. Sundhet har også en relatert betydning i matematisk logikk, hvor logiske systemer er sunne hvis og bare hvis hver formel som kan bevises i systemet er logisk gyldig med hensyn til systemets semantikk.
Arkimedisk spiral: Archimedean-spiralen er en spiral oppkalt etter den greske matematikeren Archimedes fra det 3. århundre f.Kr. Det er stedet som tilsvarer stedene over tid for et punkt som beveger seg bort fra et fast punkt med konstant hastighet langs en linje som roterer med konstant vinkelhastighet. Tilsvarende kan det i polare koordinater ( r , θ ) beskrives ved ligningen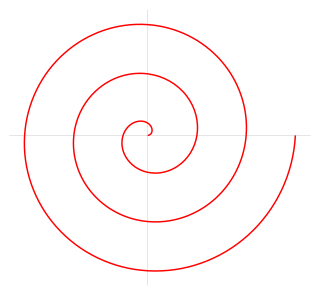
Aritmetisk gruppe: I matematikk er en aritmetisk gruppe en gruppe oppnådd som heltallene til en algebraisk gruppe, for eksempel De oppstår naturlig i studiet av aritmetiske egenskaper til kvadratiske former og andre klassiske emner i tallteori. De gir også opphav til veldig interessante eksempler på Riemannian manifolds og er derfor objekter av interesse for differensial geometri og topologi. Til slutt blir disse to emnene med i teorien om automatiske former som er grunnleggende i moderne tallteori.