Cartesian product

Kartesisk produkt: I matematikk, spesielt settteori, er det kartesiske produktet av to sett A og B , betegnet A × B , settet av alle ordnede par ( a , b ) hvor a er i A og b er i B. Når det gjelder set-builder-notasjon, det vil si
Kartesiske refleksjoner: Cartesian Reflections er en bok fra 2008 av filosofen John Cottingham. Arbeidet består av flere essays som omhandler forskjellige temaer, for eksempel René Descartes syn på dyr, hans holdning til dualismen i sinn og kropp og forholdet mellom tankene hans og Baruch Spinozas.
Kartesisk selv: I filosofien er det kartesiske selvet , en del av et tankeeksperiment, et individs sinn, atskilt fra kroppen og omverdenen, og tenker på seg selv og dets eksistens. Det skilles fra den kartesiske andre, alt annet enn det kartesiske jeget. I følge filosofen Rene Descartes er det et skille som er iboende for bevisstheten, slik at man aldri kan bygge bro mellom egen bevissthet og andres.
Kartesisk tvil: Kartesisk tvil er en form for metodisk skepsis knyttet til skrifter og metodikk til René Descartes. Kartesisk tvil er også kjent som kartesisk skepsis , metodisk tvil , metodisk skepsis , universell tvil , systematisk tvil eller hyperbolsk tvil .
Kartesisk skyskraper: Den kartesiske himmelskraperen , designet av Le Corbusier i 1938, er en type tårn kjent for sin moderne og rasjonelle design. Denne typen moderne administrasjonsbygning har sin opprinnelse i de første skissene til Pavillon de l'Esprit Nouveau i 1919, som foreslo en korsform for skyskrapere, som utstrålte lys og stabilitet. I prinsippet tilpasser korsformede planen seg ikke til solens vei, som bare har en akse. Ved å studere videre, ble det sett at med denne symmetriske formen om to akser, mottar korsskyskraperen ikke sollys på sine nordvendte sider.
Kartesisk teater: " Kartesisk teater " er et spottende begrep som ble oppfunnet av filosof og kognitiv forsker Daniel Dennett for å referere punktlig til et definerende aspekt ved det han kaller kartesisk materialisme, som han anser for å være de ofte ukjente restene av kartesisk dualisme i moderne materialistiske teorier om sinnet.
Kartesisk teater: " Kartesisk teater " er et spottende begrep som ble oppfunnet av filosof og kognitiv forsker Daniel Dennett for å referere punktlig til et definerende aspekt ved det han kaller kartesisk materialisme, som han anser for å være de ofte ukjente restene av kartesisk dualisme i moderne materialistiske teorier om sinnet.
Kartesisk angst: Kartesisk angst refererer til forestillingen om at den vestlige sivilisasjonen, siden René Descartes stilte sin innflytelsesrike form for kropp-sinn-dualisme, har lidd av en lengsel etter ontologisk sikkerhet, eller følelsen av at vitenskapelige metoder, og spesielt studiet av verden som en ting som er atskilt fra oss selv, skal kunne lede oss til en fast og uforanderlig kunnskap om oss selv og verden rundt oss. Begrepet er oppkalt etter Descartes på grunn av hans velkjente vektlegging av "sinn" som er forskjellig fra "kropp", "selv" som forskjellig fra "annet".
Kartesisk koordinatsystem: Et kartesisk koordinatsystem i et plan er et koordinatsystem som spesifiserer hvert punkt unikt med et par numeriske koordinater , som er de signerte avstandene til punktet fra to faste vinkelrett orienterte linjer, målt i samme lengdeenhet. Hver referanselinje kalles en koordinatakse eller bare aksen til systemet, og punktet der de møtes er dens opprinnelse , ved ordnet par (0, 0) . Koordinatene kan også defineres som posisjonene til punktets vinkelrette projeksjoner på de to aksene, uttrykt som signerte avstander fra opprinnelsen.
Kartesisk koordinatsystem: Et kartesisk koordinatsystem i et plan er et koordinatsystem som spesifiserer hvert punkt unikt med et par numeriske koordinater , som er de signerte avstandene til punktet fra to faste vinkelrett orienterte linjer, målt i samme lengdeenhet. Hver referanselinje kalles en koordinatakse eller bare aksen til systemet, og punktet der de møtes er dens opprinnelse , ved ordnet par (0, 0) . Koordinatene kan også defineres som posisjonene til punktets vinkelrette projeksjoner på de to aksene, uttrykt som signerte avstander fra opprinnelsen.
Kartesisk sirkel: Den kartesiske sirkelen er en potensiell feil i resonnement tilskrevet René Descartes.
Kartesisk lukket kategori: I kategoriteori er en kategori kartesisk lukket hvis noen form for morfisme definert på et produkt av to objekter grovt sett kan identifiseres naturlig med en morfisme definert på en av faktorene. Disse kategoriene er spesielt viktige i matematisk logikk og teorien om programmering, ved at deres interne språk er den ganske enkelt skrevet lambda -beregningen. De generaliseres av lukkede monoidale kategorier, hvis indre språk, lineære type systemer, er egnet for både kvante- og klassisk beregning.
Kartesisk lukket kategori: I kategoriteori er en kategori kartesisk lukket hvis noen form for morfisme definert på et produkt av to objekter grovt sett kan identifiseres naturlig med en morfisme definert på en av faktorene. Disse kategoriene er spesielt viktige i matematisk logikk og teorien om programmering, ved at deres interne språk er den ganske enkelt skrevet lambda -beregningen. De generaliseres av lukkede monoidale kategorier, hvis indre språk, lineære type systemer, er egnet for både kvante- og klassisk beregning.
Kartesisk lukket kategori: I kategoriteori er en kategori kartesisk lukket hvis noen form for morfisme definert på et produkt av to objekter grovt sett kan identifiseres naturlig med en morfisme definert på en av faktorene. Disse kategoriene er spesielt viktige i matematisk logikk og teorien om programmering, ved at deres interne språk er den ganske enkelt skrevet lambda -beregningen. De generaliseres av lukkede monoidale kategorier, hvis indre språk, lineære type systemer, er egnet for både kvante- og klassisk beregning.
Kartesisk lukket kategori: I kategoriteori er en kategori kartesisk lukket hvis noen form for morfisme definert på et produkt av to objekter grovt sett kan identifiseres naturlig med en morfisme definert på en av faktorene. Disse kategoriene er spesielt viktige i matematisk logikk og teorien om programmering, ved at deres interne språk er den ganske enkelt skrevet lambda -beregningen. De generaliseres av lukkede monoidale kategorier, hvis indre språk, lineære type systemer, er egnet for både kvante- og klassisk beregning.
Kartesisk koordinatsystem: Et kartesisk koordinatsystem i et plan er et koordinatsystem som spesifiserer hvert punkt unikt med et par numeriske koordinater , som er de signerte avstandene til punktet fra to faste vinkelrett orienterte linjer, målt i samme lengdeenhet. Hver referanselinje kalles en koordinatakse eller bare aksen til systemet, og punktet der de møtes er dens opprinnelse , ved ordnet par (0, 0) . Koordinatene kan også defineres som posisjonene til punktets vinkelrette projeksjoner på de to aksene, uttrykt som signerte avstander fra opprinnelsen.
Kartesisk koordinatsystem: Et kartesisk koordinatsystem i et plan er et koordinatsystem som spesifiserer hvert punkt unikt med et par numeriske koordinater , som er de signerte avstandene til punktet fra to faste vinkelrett orienterte linjer, målt i samme lengdeenhet. Hver referanselinje kalles en koordinatakse eller bare aksen til systemet, og punktet der de møtes er dens opprinnelse , ved ordnet par (0, 0) . Koordinatene kan også defineres som posisjonene til punktets vinkelrette projeksjoner på de to aksene, uttrykt som signerte avstander fra opprinnelsen.
Kartesisk koordinatsystem: Et kartesisk koordinatsystem i et plan er et koordinatsystem som spesifiserer hvert punkt unikt med et par numeriske koordinater , som er de signerte avstandene til punktet fra to faste vinkelrett orienterte linjer, målt i samme lengdeenhet. Hver referanselinje kalles en koordinatakse eller bare aksen til systemet, og punktet der de møtes er dens opprinnelse , ved ordnet par (0, 0) . Koordinatene kan også defineres som posisjonene til punktets vinkelrette projeksjoner på de to aksene, uttrykt som signerte avstander fra opprinnelsen.
Cogito, ergo sum: Cogito, ergo sum er en filosofisk uttalelse som ble fremsatt på latin av René Descartes, vanligvis oversatt til engelsk som " I think, derfor I am ". Uttrykket dukket opprinnelig opp på fransk som je pense , donc je suis i Discourse on the Method , for å nå et bredere publikum enn latin ville ha tillatt. Det dukket opp på latin i hans senere filosofiprinsipper . Som Descartes forklarte det, "kan vi ikke tvile på vår eksistens mens vi tviler." En fyldigere versjon, artikulert av Antoine Léonard Thomas, fanger passende Descartes intensjon: dubito, ergo cogito, ergo sum . Dictum er også noen ganger referert til som cogito .
Kartesisk koordinatsystem: Et kartesisk koordinatsystem i et plan er et koordinatsystem som spesifiserer hvert punkt unikt med et par numeriske koordinater , som er de signerte avstandene til punktet fra to faste vinkelrett orienterte linjer, målt i samme lengdeenhet. Hver referanselinje kalles en koordinatakse eller bare aksen til systemet, og punktet der de møtes er dens opprinnelse , ved ordnet par (0, 0) . Koordinatene kan også defineres som posisjonene til punktets vinkelrette projeksjoner på de to aksene, uttrykt som signerte avstander fra opprinnelsen.
Kartesisk koordinatsystem: Et kartesisk koordinatsystem i et plan er et koordinatsystem som spesifiserer hvert punkt unikt med et par numeriske koordinater , som er de signerte avstandene til punktet fra to faste vinkelrett orienterte linjer, målt i samme lengdeenhet. Hver referanselinje kalles en koordinatakse eller bare aksen til systemet, og punktet der de møtes er dens opprinnelse , ved ordnet par (0, 0) . Koordinatene kan også defineres som posisjonene til punktets vinkelrette projeksjoner på de to aksene, uttrykt som signerte avstander fra opprinnelsen.
Kartesisk koordinatrobot: En kartesisk koordinatrobot er en industrirobot hvis tre hovedakser for kontroll er lineære og er vinkelrett på hverandre. De tre glideleddene tilsvarer å bevege håndleddet opp-ned, inn-ut, frem og tilbake. Blant andre fordeler forenkler dette mekaniske arrangementet Robot -kontrollarmen. Den har høy pålitelighet og presisjon når den opererer i tredimensjonalt rom. Som et robotkoordinatsystem er det også effektivt for horisontale reiser og for stabling av søppelbøtter.
Kartesisk koordinatsystem: Et kartesisk koordinatsystem i et plan er et koordinatsystem som spesifiserer hvert punkt unikt med et par numeriske koordinater , som er de signerte avstandene til punktet fra to faste vinkelrett orienterte linjer, målt i samme lengdeenhet. Hver referanselinje kalles en koordinatakse eller bare aksen til systemet, og punktet der de møtes er dens opprinnelse , ved ordnet par (0, 0) . Koordinatene kan også defineres som posisjonene til punktets vinkelrette projeksjoner på de to aksene, uttrykt som signerte avstander fra opprinnelsen.
Kartesisk koordinatsystem: Et kartesisk koordinatsystem i et plan er et koordinatsystem som spesifiserer hvert punkt unikt med et par numeriske koordinater , som er de signerte avstandene til punktet fra to faste vinkelrett orienterte linjer, målt i samme lengdeenhet. Hver referanselinje kalles en koordinatakse eller bare aksen til systemet, og punktet der de møtes er dens opprinnelse , ved ordnet par (0, 0) . Koordinatene kan også defineres som posisjonene til punktets vinkelrette projeksjoner på de to aksene, uttrykt som signerte avstander fra opprinnelsen.
Kartesisk koordinatsystem: Et kartesisk koordinatsystem i et plan er et koordinatsystem som spesifiserer hvert punkt unikt med et par numeriske koordinater , som er de signerte avstandene til punktet fra to faste vinkelrett orienterte linjer, målt i samme lengdeenhet. Hver referanselinje kalles en koordinatakse eller bare aksen til systemet, og punktet der de møtes er dens opprinnelse , ved ordnet par (0, 0) . Koordinatene kan også defineres som posisjonene til punktets vinkelrette projeksjoner på de to aksene, uttrykt som signerte avstander fra opprinnelsen.
Ond demon: Den onde demonen , også kjent som Descartes 'demon , ondsinnede demon og onde geni , er et epistemologisk konsept som har en fremtredende rolle i den kartesiske filosofien. I den første av sine meditasjoner fra 1641 om første filosofi fra 1641 forestiller Descartes seg at en ond demon med "ytterste makt og list har brukt all sin energi for å lure meg." Denne onde demonen forestiller seg å presentere en fullstendig illusjon av en ytre verden, slik at Descartes kan si: "Jeg skal tro at himmelen, luften, jorden, farger, former, lyder og alle ytre ting bare er drømmenes vrangforestillinger som han har tenkt for å fange min dom. Jeg skal betrakte meg selv som å ikke ha hender eller øyne, eller kjøtt, eller blod eller sanser, men som falskt tro på at jeg har alt dette. "
Kartesisk dykker: En kartesisk dykker eller kartesisk djevel er et klassisk vitenskapelig eksperiment som demonstrerer oppdriftsprinsippet og den ideelle gassloven. Den første skriftlige beskrivelsen av denne enheten er gitt av Raffaello Magiotti, i sin bok Renitenza certissima dell'acqua alla compressione utgitt i 1648. Den er oppkalt etter René Descartes som leketøyet som det sies å ha blitt oppfunnet av ham.
Tilbaketrekking (kategoriteori): I kategoriteori, en gren av matematikk, er en tilbaketrekning grensen for et diagram som består av to morfisme f : X → Z og g : Y → Z med et felles kodomen. Tilbaketrekkingen er ofte skrevet P = X × Z Y
Kartesisk koordinatsystem: Et kartesisk koordinatsystem i et plan er et koordinatsystem som spesifiserer hvert punkt unikt med et par numeriske koordinater , som er de signerte avstandene til punktet fra to faste vinkelrett orienterte linjer, målt i samme lengdeenhet. Hver referanselinje kalles en koordinatakse eller bare aksen til systemet, og punktet der de møtes er dens opprinnelse , ved ordnet par (0, 0) . Koordinatene kan også defineres som posisjonene til punktets vinkelrette projeksjoner på de to aksene, uttrykt som signerte avstander fra opprinnelsen.
Kartesisk koordinatsystem: Et kartesisk koordinatsystem i et plan er et koordinatsystem som spesifiserer hvert punkt unikt med et par numeriske koordinater , som er de signerte avstandene til punktet fra to faste vinkelrett orienterte linjer, målt i samme lengdeenhet. Hver referanselinje kalles en koordinatakse eller bare aksen til systemet, og punktet der de møtes er dens opprinnelse , ved ordnet par (0, 0) . Koordinatene kan også defineres som posisjonene til punktets vinkelrette projeksjoner på de to aksene, uttrykt som signerte avstander fra opprinnelsen.
Kartesisk dykker: En kartesisk dykker eller kartesisk djevel er et klassisk vitenskapelig eksperiment som demonstrerer oppdriftsprinsippet og den ideelle gassloven. Den første skriftlige beskrivelsen av denne enheten er gitt av Raffaello Magiotti, i sin bok Renitenza certissima dell'acqua alla compressione utgitt i 1648. Den er oppkalt etter René Descartes som leketøyet som det sies å ha blitt oppfunnet av ham.
Kartesisk tvil: Kartesisk tvil er en form for metodisk skepsis knyttet til skrifter og metodikk til René Descartes. Kartesisk tvil er også kjent som kartesisk skepsis , metodisk tvil , metodisk skepsis , universell tvil , systematisk tvil eller hyperbolsk tvil .
Kartesisk dykker: En kartesisk dykker eller kartesisk djevel er et klassisk vitenskapelig eksperiment som demonstrerer oppdriftsprinsippet og den ideelle gassloven. Den første skriftlige beskrivelsen av denne enheten er gitt av Raffaello Magiotti, i sin bok Renitenza certissima dell'acqua alla compressione utgitt i 1648. Den er oppkalt etter René Descartes som leketøyet som det sies å ha blitt oppfunnet av ham.
Sinn -kropp -dualisme: I sinnsfilosofien betegner dualisme mellom sinn og kropp enten synet på at mentale fenomener er ikke-fysiske, eller at sinnet og kroppen er forskjellige og kan skilles. Dermed omfatter den et sett med synspunkter om forholdet mellom sinn og materie, så vel som mellom subjekt og objekt, og står i kontrast med andre posisjoner, for eksempel fysikalisme og enaktivisme, i sinn -kropp -problemet.
Sinn -kropp -dualisme: I sinnsfilosofien betegner dualisme mellom sinn og kropp enten synet på at mentale fenomener er ikke-fysiske, eller at sinnet og kroppen er forskjellige og kan skilles. Dermed omfatter den et sett med synspunkter om forholdet mellom sinn og materie, så vel som mellom subjekt og objekt, og står i kontrast med andre posisjoner, for eksempel fysikalisme og enaktivisme, i sinn -kropp -problemet.
Kartesianisme: Den kartesiske metoden er det filosofiske og vitenskapelige systemet til René Descartes og den påfølgende utviklingen av andre tenkere fra det syttende århundre, særlig François Poullain de la Barre, Nicolas Malebranche og Baruch Spinoza. Descartes blir ofte sett på som den første tenkeren som understreket bruken av fornuft for å utvikle naturvitenskapene. For ham var filosofi et tenkesystem som legemliggjorde all kunnskap.
Kartesisk koordinatsystem: Et kartesisk koordinatsystem i et plan er et koordinatsystem som spesifiserer hvert punkt unikt med et par numeriske koordinater , som er de signerte avstandene til punktet fra to faste vinkelrett orienterte linjer, målt i samme lengdeenhet. Hver referanselinje kalles en koordinatakse eller bare aksen til systemet, og punktet der de møtes er dens opprinnelse , ved ordnet par (0, 0) . Koordinatene kan også defineres som posisjonene til punktets vinkelrette projeksjoner på de to aksene, uttrykt som signerte avstander fra opprinnelsen.
Kartesisk sirkel: Den kartesiske sirkelen er en potensiell feil i resonnement tilskrevet René Descartes.
Kartesisk genetisk programmering: Kartesisk genetisk programmering er en form for genetisk programmering som bruker en grafrepresentasjon for å kode dataprogrammer. Det vokste fra en metode for å utvikle digitale kretser utviklet av Julian F. Miller og Peter Thomson i 1997. Begrepet 'kartesisk genetisk programmering' dukket først opp i 1999 og ble foreslått som en generell form for genetisk programmering i 2000. Det kalles 'kartesisk 'fordi det representerer et program som bruker et todimensjonalt rutenett med noder.
Analytisk geometri: I klassisk matematikk er analytisk geometri , også kjent som koordinatgeometri eller kartesisk geometri , studiet av geometri ved hjelp av et koordinatsystem. Dette står i kontrast til syntetisk geometri.
Vanlig rutenett: Et vanlig rutenett er en tessellasjon av n -dimensjonalt euklidisk rom ved kongruente parallellotoper. Denne rutenettet vises på grafpapir og kan brukes i endelige elementanalyser, endelige volummetoder, endelige forskjellsmetoder og generelt for diskretisering av parameterrom. Siden derivatene av feltvariabler beleilig kan uttrykkes som begrensede forskjeller, vises strukturerte rutenett hovedsakelig i endelige forskjellsmetoder. Ustrukturerte rutenett gir mer fleksibilitet enn strukturerte rutenett og er derfor veldig nyttige i metoder for endelig element og begrenset volum.
Bli med (SQL): En join -klausul i SQL - tilsvarende en join -operasjon i relasjonsalgebra - kombinerer kolonner fra en eller flere tabeller til en ny tabell. ANSI-standard SQL angir fem typer JOIN : INNER , LEFT OUTER , RIGHT OUTER , FULL OUTER og CROSS .
Verden (bok): Verden , også kalt Treatise on the Light , er en bok av René Descartes (1596–1650). Skrevet mellom 1629 og 1633, inneholder den en nesten komplett versjon av filosofien hans, fra metode, til metafysikk, til fysikk og biologi.
Kartesisk lingvistikk: Begrepet kartesisk lingvistikk ble laget med publiseringen av Cartesian Linguistics: A Chapter in the History of Rationalist Thought (1966), en bok om lingvistikk av Noam Chomsky. Ordet "kartesisk" er adjektivet som gjelder René Descartes, en fremtredende filosof fra 1600-tallet. I stedet for å begrense seg til arbeidet til Descartes, undersøker Chomsky imidlertid andre forfattere som er interessert i rasjonalistisk tankegang. Spesielt diskuterer Chomsky Port-Royal Grammar (1660), en bok som viser noen av hans egne ideer om universell grammatikk.
Kartesisk lingvistikk: Begrepet kartesisk lingvistikk ble laget med publiseringen av Cartesian Linguistics: A Chapter in the History of Rationalist Thought (1966), en bok om lingvistikk av Noam Chomsky. Ordet "kartesisk" er adjektivet som gjelder René Descartes, en fremtredende filosof fra 1600-tallet. I stedet for å begrense seg til arbeidet til Descartes, undersøker Chomsky imidlertid andre forfattere som er interessert i rasjonalistisk tankegang. Spesielt diskuterer Chomsky Port-Royal Grammar (1660), en bok som viser noen av hans egne ideer om universell grammatikk.
Kartesisk tvil: Kartesisk tvil er en form for metodisk skepsis knyttet til skrifter og metodikk til René Descartes. Kartesisk tvil er også kjent som kartesisk skepsis , metodisk tvil , metodisk skepsis , universell tvil , systematisk tvil eller hyperbolsk tvil .
Kartesisk materialisme: I sinnsfilosofi er kartesisk materialisme ideen om at det på et sted i hjernen er et sett med informasjon som direkte tilsvarer vår bevisste opplevelse. I motsetning til navnet er ikke kartesisk materialisme et syn som ble holdt av eller formulert av René Descartes, som snarere abonnerte på en form for substansdualisme.
Kartesisk materialisme: I sinnsfilosofi er kartesisk materialisme ideen om at det på et sted i hjernen er et sett med informasjon som direkte tilsvarer vår bevisste opplevelse. I motsetning til navnet er ikke kartesisk materialisme et syn som ble holdt av eller formulert av René Descartes, som snarere abonnerte på en form for substansdualisme.
Kartesisk monoid: En kartesisk monoid er en monoid, med tilleggsstruktur for sammenkoblings- og projeksjonsoperatorer. Det ble først formulert av Dana Scott og Joachim Lambek uavhengig.
Cartesian monoidal kategori: I matematikk, spesielt på feltet kjent som kategoriteori, er en monoid kategori der det monoidale ("tensor") produktet er det kategoriske produktet, kalt en kartesisk monoid kategori . Enhver kategori med begrensede produkter kan betraktes som en kartesisk monoid kategori. I en hvilken som helst kartesisk monoid kategori er terminalobjektet den monoidale enheten. Dosalt kalles en monoidal endelig koproduktkategori med den monoidale strukturen gitt av koproduktet og enheten det opprinnelige objektet, en cocartesian monoidal kategori , og enhver endelig koproduktkategori kan betraktes som en cocartesian monoidal kategori.
Fibrert kategori: Fibrerte kategorier er abstrakte enheter i matematikk som brukes til å gi et generelt rammeverk for nedstigningsteori. De formaliserer de forskjellige situasjonene i geometri og algebra der inverse bilder av objekter som vektorgrupper kan defineres. Som et eksempel er det for hvert topologisk rom kategorien vektorgrupper på rommet, og for hvert sammenhengende kart fra et topologisk rom X til et annet topologisk rom Y er tilknyttet tilbaketrekningsfunksjonen som tar bunter på Y til bunter på X. Fibrerte kategorier formaliserer systemet som består av disse kategoriene og omvendte bildefunksjoner. Lignende oppsett vises i forskjellige former for matematikk, spesielt i algebraisk geometri, som er konteksten der fibre kategorier opprinnelig dukket opp. Fiberkategorier brukes til å definere stabler, som er fiberkategorier med "nedstigning". Fibrasjoner spiller også en viktig rolle i kategorisk semantikk for typeteori, og spesielt avhengige typeteorier.
Kartesisk koordinatsystem: Et kartesisk koordinatsystem i et plan er et koordinatsystem som spesifiserer hvert punkt unikt med et par numeriske koordinater , som er de signerte avstandene til punktet fra to faste vinkelrett orienterte linjer, målt i samme lengdeenhet. Hver referanselinje kalles en koordinatakse eller bare aksen til systemet, og punktet der de møtes er dens opprinnelse , ved ordnet par (0, 0) . Koordinatene kan også defineres som posisjonene til punktets vinkelrette projeksjoner på de to aksene, uttrykt som signerte avstander fra opprinnelsen.
Kartesisk annet: I filosofien er den kartesiske andre , en del av et tankeeksperiment, noe annet enn sinnet til den enkelte tenker om eksperimentet. Den andre inkluderer individets egen kropp. I følge filosofen Descartes er det et skille som er iboende for bevisstheten, slik at du aldri kan bygge bro mellom din egen og en annen bevissthet.
Kartesisk oval: I geometri er en kartesisk oval en plan kurve som består av punkter som har samme lineære kombinasjon av avstander fra to faste punkter. Disse kurvene er oppkalt etter René Descartes, som brukte dem i optikk.
Kartesisk oval: I geometri er en kartesisk oval en plan kurve som består av punkter som har samme lineære kombinasjon av avstander fra to faste punkter. Disse kurvene er oppkalt etter René Descartes, som brukte dem i optikk.
Kartesiske parallelle manipulatorer: I robotikk er kartesiske parallelle manipulatorer manipulatorer som beveger en plattform ved hjelp av parallellkoblede kinematiske koblinger (`` lemmer '') oppstilt med et kartesisk koordinatsystem. Flere lemmer kobler den bevegelige plattformen til en base. Hvert lem drives av en lineær aktuator og de lineære aktuatorene er gjensidig vinkelrett. Begrepet `parallell 'refererer her til måten de kinematiske koblingene settes sammen på, det er ikke geometrisk parallelt; dvs. like store linjer.
Kartesianisme: Den kartesiske metoden er det filosofiske og vitenskapelige systemet til René Descartes og den påfølgende utviklingen av andre tenkere fra det syttende århundre, særlig François Poullain de la Barre, Nicolas Malebranche og Baruch Spinoza. Descartes blir ofte sett på som den første tenkeren som understreket bruken av fornuft for å utvikle naturvitenskapene. For ham var filosofi et tenkesystem som legemliggjorde all kunnskap.
Mekaniske forklaringer på gravitasjon: Mekaniske forklaringer på gravitasjon er forsøk på å forklare tyngdekraftens virkning ved hjelp av grunnleggende mekaniske prosesser, for eksempel trykkrefter forårsaket av trykk, uten bruk av handling på avstand. Disse teoriene ble utviklet fra 1500- til 1800 -tallet i forbindelse med eteren. Imidlertid regnes slike modeller ikke lenger som levedyktige teorier i det vanlige vitenskapelige samfunnet, og generell relativitet er nå standardmodellen for å beskrive gravitasjon uten bruk av handlinger på avstand. Moderne "kvantegravitasjon" -hypoteser prøver også å beskrive tyngdekraften ved mer grunnleggende prosesser som partikkelfelt, men de er ikke basert på klassisk mekanikk.
Kartesisk koordinatsystem: Et kartesisk koordinatsystem i et plan er et koordinatsystem som spesifiserer hvert punkt unikt med et par numeriske koordinater , som er de signerte avstandene til punktet fra to faste vinkelrett orienterte linjer, målt i samme lengdeenhet. Hver referanselinje kalles en koordinatakse eller bare aksen til systemet, og punktet der de møtes er dens opprinnelse , ved ordnet par (0, 0) . Koordinatene kan også defineres som posisjonene til punktets vinkelrette projeksjoner på de to aksene, uttrykt som signerte avstander fra opprinnelsen.
Kartesisk koordinatsystem: Et kartesisk koordinatsystem i et plan er et koordinatsystem som spesifiserer hvert punkt unikt med et par numeriske koordinater , som er de signerte avstandene til punktet fra to faste vinkelrett orienterte linjer, målt i samme lengdeenhet. Hver referanselinje kalles en koordinatakse eller bare aksen til systemet, og punktet der de møtes er dens opprinnelse , ved ordnet par (0, 0) . Koordinatene kan også defineres som posisjonene til punktets vinkelrette projeksjoner på de to aksene, uttrykt som signerte avstander fra opprinnelsen.
Kartesisk koordinatsystem: Et kartesisk koordinatsystem i et plan er et koordinatsystem som spesifiserer hvert punkt unikt med et par numeriske koordinater , som er de signerte avstandene til punktet fra to faste vinkelrett orienterte linjer, målt i samme lengdeenhet. Hver referanselinje kalles en koordinatakse eller bare aksen til systemet, og punktet der de møtes er dens opprinnelse , ved ordnet par (0, 0) . Koordinatene kan også defineres som posisjonene til punktets vinkelrette projeksjoner på de to aksene, uttrykt som signerte avstander fra opprinnelsen.
Horror vacui (fysikk): I fysikk er horror vacui eller plenisme , vanligvis uttalt som " naturen avskyr et vakuum ", et postulat tilskrevet Aristoteles, som artikulerte en tro, senere kritisert av atomismen til Epicurus og Lucretius, at naturen ikke inneholder støvsugere fordi den tettere omgivelsen materiell kontinuum ville umiddelbart fylle sjeldenheten til et begynnende tomrom. Han argumenterte også mot tomrommet i en mer abstrakt forstand, for eksempel at et tomrom i seg selv per definisjon er ingenting, og etter Platon kan ingenting med rette sies å eksistere. Videre, for så vidt det ville være uten egenskaper, kunne det verken oppstå av sansene, eller dets antagelse kunne gi ytterligere forklaringskraft. Helt av Alexandria utfordret teorien i det første århundre e.Kr., men hans forsøk på å skape et kunstig vakuum mislyktes. Teorien ble diskutert i sammenheng med væskemekanikken fra 1600-tallet, blant andre av Thomas Hobbes og Robert Boyle, og gjennom begynnelsen av 1700-tallet av Sir Isaac Newton og Gottfried Leibniz.
Kartesisk produkt: I matematikk, spesielt settteori, er det kartesiske produktet av to sett A og B , betegnet A × B , settet av alle ordnede par ( a , b ) hvor a er i A og b er i B. Når det gjelder set-builder-notasjon, det vil si
Kartesisk produkt: I matematikk, spesielt settteori, er det kartesiske produktet av to sett A og B , betegnet A × B , settet av alle ordnede par ( a , b ) hvor a er i A og b er i B. Når det gjelder set-builder-notasjon, det vil si
Kartesisk produkt: I matematikk, spesielt settteori, er det kartesiske produktet av to sett A og B , betegnet A × B , settet av alle ordnede par ( a , b ) hvor a er i A og b er i B. Når det gjelder set-builder-notasjon, det vil si
Kartesisk produkt av grafer: I grafteorien har det kartesiske produktet G H for grafene G og H er en graf slik at toppunktet av G H er det kartesiske produktet V ( G ) × V ( H ); og to hjørner og er tilstøtende i G H hvis og bare hvis enten u = v og u ' ligger ved siden av v' i H , eller u ' = v' og u ligger ved siden av v i G.
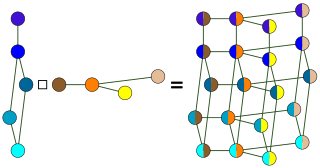Kartesisk produkt: I matematikk, spesielt settteori, er det kartesiske produktet av to sett A og B , betegnet A × B , settet av alle ordnede par ( a , b ) hvor a er i A og b er i B. Når det gjelder set-builder-notasjon, det vil si
Kartesisk koordinatrobot: En kartesisk koordinatrobot er en industrirobot hvis tre hovedakser for kontroll er lineære og er vinkelrett på hverandre. De tre glideleddene tilsvarer å bevege håndleddet opp-ned, inn-ut, frem og tilbake. Blant andre fordeler forenkler dette mekaniske arrangementet Robot -kontrollarmen. Den har høy pålitelighet og presisjon når den opererer i tredimensjonalt rom. Som et robotkoordinatsystem er det også effektivt for horisontale reiser og for stabling av søppelbøtter.
Kartesisk tvil: Kartesisk tvil er en form for metodisk skepsis knyttet til skrifter og metodikk til René Descartes. Kartesisk tvil er også kjent som kartesisk skepsis , metodisk tvil , metodisk skepsis , universell tvil , systematisk tvil eller hyperbolsk tvil .
Fibrert kategori: Fibrerte kategorier er abstrakte enheter i matematikk som brukes til å gi et generelt rammeverk for nedstigningsteori. De formaliserer de forskjellige situasjonene i geometri og algebra der inverse bilder av objekter som vektorgrupper kan defineres. Som et eksempel er det for hvert topologisk rom kategorien vektorgrupper på rommet, og for hvert sammenhengende kart fra et topologisk rom X til et annet topologisk rom Y er tilknyttet tilbaketrekningsfunksjonen som tar bunter på Y til bunter på X. Fibrerte kategorier formaliserer systemet som består av disse kategoriene og omvendte bildefunksjoner. Lignende oppsett vises i forskjellige former for matematikk, spesielt i algebraisk geometri, som er konteksten der fibre kategorier opprinnelig dukket opp. Fiberkategorier brukes til å definere stabler, som er fiberkategorier med "nedstigning". Fibrasjoner spiller også en viktig rolle i kategorisk semantikk for typeteori, og spesielt avhengige typeteorier.
Kartesisk selv: I filosofien er det kartesiske selvet , en del av et tankeeksperiment, et individs sinn, atskilt fra kroppen og omverdenen, og tenker på seg selv og dets eksistens. Det skilles fra den kartesiske andre, alt annet enn det kartesiske jeget. I følge filosofen Rene Descartes er det et skille som er iboende for bevisstheten, slik at man aldri kan bygge bro mellom egen bevissthet og andres.
Kartesisk tvil: Kartesisk tvil er en form for metodisk skepsis knyttet til skrifter og metodikk til René Descartes. Kartesisk tvil er også kjent som kartesisk skepsis , metodisk tvil , metodisk skepsis , universell tvil , systematisk tvil eller hyperbolsk tvil .
Kartesisk skyskraper: Den kartesiske himmelskraperen , designet av Le Corbusier i 1938, er en type tårn kjent for sin moderne og rasjonelle design. Denne typen moderne administrasjonsbygning har sin opprinnelse i de første skissene til Pavillon de l'Esprit Nouveau i 1919, som foreslo en korsform for skyskrapere, som utstrålte lys og stabilitet. I prinsippet tilpasser korsformede planen seg ikke til solens vei, som bare har en akse. Ved å studere videre, ble det sett at med denne symmetriske formen om to akser, mottar korsskyskraperen ikke sollys på sine nordvendte sider.
Kartesisk koordinatsystem: Et kartesisk koordinatsystem i et plan er et koordinatsystem som spesifiserer hvert punkt unikt med et par numeriske koordinater , som er de signerte avstandene til punktet fra to faste vinkelrett orienterte linjer, målt i samme lengdeenhet. Hver referanselinje kalles en koordinatakse eller bare aksen til systemet, og punktet der de møtes er dens opprinnelse , ved ordnet par (0, 0) . Koordinatene kan også defineres som posisjonene til punktets vinkelrette projeksjoner på de to aksene, uttrykt som signerte avstander fra opprinnelsen.
Kartesisk produkt: I matematikk, spesielt settteori, er det kartesiske produktet av to sett A og B , betegnet A × B , settet av alle ordnede par ( a , b ) hvor a er i A og b er i B. Når det gjelder set-builder-notasjon, det vil si
Tilbaketrekking (kategoriteori): I kategoriteori, en gren av matematikk, er en tilbaketrekning grensen for et diagram som består av to morfisme f : X → Z og g : Y → Z med et felles kodomen. Tilbaketrekkingen er ofte skrevet P = X × Z Y
Kartesisk tensor: I geometri og lineær algebra bruker en kartesisk tensor et ortonormalt grunnlag for å representere en tensor i et euklidisk rom i form av komponenter. Konvertering av en tensors komponenter fra en slik basis til en annen er gjennom en ortogonal transformasjon.
Kartesisk teater: " Kartesisk teater " er et spottende begrep som ble oppfunnet av filosof og kognitiv forsker Daniel Dennett for å referere punktlig til et definerende aspekt ved det han kaller kartesisk materialisme, som han anser for å være de ofte ukjente restene av kartesisk dualisme i moderne materialistiske teorier om sinnet.
Kartesisk teater: " Kartesisk teater " er et spottende begrep som ble oppfunnet av filosof og kognitiv forsker Daniel Dennett for å referere punktlig til et definerende aspekt ved det han kaller kartesisk materialisme, som han anser for å være de ofte ukjente restene av kartesisk dualisme i moderne materialistiske teorier om sinnet.
Kartesisk tre: I informatikk er et kartesisk tre et binært tre som stammer fra en tallrekke; det kan entydig defineres ut fra egenskapene at det er haugordnet og at en symmetrisk (i rekkefølge) traversal av treet returnerer den opprinnelige sekvensen. Kartesiske trær ble introdusert av Vuillemin (1980) i sammenheng med datastrukturer for geometrisk område -søk, og har også blitt brukt i definisjonen av treap og randomiserte binære søketre -datastrukturer for binære søkeproblemer. Det kartesiske treet for en sekvens kan konstrueres i lineær tid ved hjelp av en stabelbasert algoritme for å finne alle nærmeste mindre verdier i en sekvens.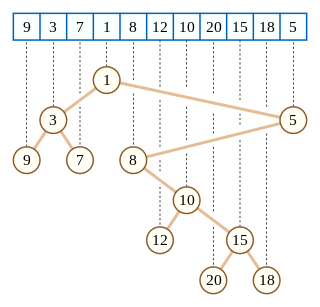
Mekaniske forklaringer på gravitasjon: Mekaniske forklaringer på gravitasjon er forsøk på å forklare tyngdekraftens virkning ved hjelp av grunnleggende mekaniske prosesser, for eksempel trykkrefter forårsaket av trykk, uten bruk av handling på avstand. Disse teoriene ble utviklet fra 1500- til 1800 -tallet i forbindelse med eteren. Imidlertid regnes slike modeller ikke lenger som levedyktige teorier i det vanlige vitenskapelige samfunnet, og generell relativitet er nå standardmodellen for å beskrive gravitasjon uten bruk av handlinger på avstand. Moderne "kvantegravitasjon" -hypoteser prøver også å beskrive tyngdekraften ved mer grunnleggende prosesser som partikkelfelt, men de er ikke basert på klassisk mekanikk.
Kartesianisme: Den kartesiske metoden er det filosofiske og vitenskapelige systemet til René Descartes og den påfølgende utviklingen av andre tenkere fra det syttende århundre, særlig François Poullain de la Barre, Nicolas Malebranche og Baruch Spinoza. Descartes blir ofte sett på som den første tenkeren som understreket bruken av fornuft for å utvikle naturvitenskapene. For ham var filosofi et tenkesystem som legemliggjorde all kunnskap.
Kartesianisme: Den kartesiske metoden er det filosofiske og vitenskapelige systemet til René Descartes og den påfølgende utviklingen av andre tenkere fra det syttende århundre, særlig François Poullain de la Barre, Nicolas Malebranche og Baruch Spinoza. Descartes blir ofte sett på som den første tenkeren som understreket bruken av fornuft for å utvikle naturvitenskapene. For ham var filosofi et tenkesystem som legemliggjorde all kunnskap.
Cartesio Oktató és Szolgáltató bt: Cartesio Oktató és Szolgáltató bt (2008) C-210/06 er en europeisk selskapsrettssak om etableringsfriheten.
Cartesio Oktató és Szolgáltató bt: Cartesio Oktató és Szolgáltató bt (2008) C-210/06 er en europeisk selskapsrettssak om etableringsfriheten.
Cartesio Oktató és Szolgáltató bt: Cartesio Oktató és Szolgáltató bt (2008) C-210/06 er en europeisk selskapsrettssak om etableringsfriheten.
René Descartes: René Descartes var en fransk filosof, matematiker og vitenskapsmann som oppfant analytisk geometri, og koblet de tidligere separate feltene geometri og algebra. Han tilbrakte en stor del av sitt arbeidsliv i Den nederlandske republikk, og tjente først den nederlandske statens hær av Maurice of Nassau, prinsen av Orange og Stadtholder i De forente provinser. En av de mest bemerkelsesverdige intellektuelle figurene i den nederlandske gullalderen, Descartes blir også ansett som en av grunnleggerne av moderne filosofi.
René Descartes: René Descartes var en fransk filosof, matematiker og vitenskapsmann som oppfant analytisk geometri, og koblet de tidligere separate feltene geometri og algebra. Han tilbrakte en stor del av sitt arbeidsliv i Den nederlandske republikk, og tjente først den nederlandske statens hær av Maurice of Nassau, prinsen av Orange og Stadtholder i De forente provinser. En av de mest bemerkelsesverdige intellektuelle figurene i den nederlandske gullalderen, Descartes blir også ansett som en av grunnleggerne av moderne filosofi.
Kondroitinsulfat: Kondroitinsulfat er et sulfatert glykosaminoglykan (GAG) sammensatt av en kjede med vekslende sukker. Det er vanligvis funnet festet til proteiner som en del av en proteoglykan. En kondroitinkjede kan ha over 100 individuelle sukkerarter, som hver kan sulfateres i varierende posisjoner og mengder. Kondroitinsulfat er en viktig strukturell komponent i brusk, og gir mye av dets motstand mot kompresjon. Sammen med glukosamin har kondroitinsulfat blitt et mye brukt kosttilskudd for behandling av slitasjegikt.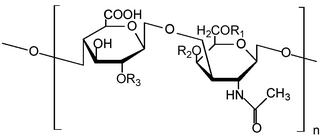
Ric Cartey: Whaley Thomas Cartey bedre kjent som Ric Cartey var en amerikansk rockabilly -musiker og låtskriver. Han dannet en duo med gitarist Charlie Broome som opptrådte lokalt. Ric og Charlies band ble kalt Jiva-Tones . Han var mest kjent som medforfatter av Carole Joyner av hiten "Young Love", en populær sang som ble utgitt i 1956. Først utgitt som singel av ham og hans band The Jiva-Tones i 1956, B-siden var "'Oooh -Eeee ". Han ble signert en innspillingskontrakt til RCA Victor. I 1958 signerte han med NRC.
Cartford Bridge: Cartford Bridge er en enkelsporet bomvei i det engelske fylket Lancashire. Den ble bygget i 1831, og strekker seg over elven Wyre, som forbinder Little Eccleston-with-Larbreck, i bydelen Fylde, på sørsiden av elven, til Out Rawcliffe, i bydelen Wyre, på nordsiden, og bærer begge biler og gangtrafikk på Cartford Lane. Bompengene er £ 1 for kjøretøy som overstiger fem tonn, 70p for kjøretøyer som overstiger to tonn, 50p for motoriserte kjøretøyer som ikke overstiger to tonn, og 20p for tohjulede kjøretøyer. I 1974 var det en av seksten bompenger på hovedveier i England. Den er 137 meter lang.
Carth Onasi: Carth Onasi er en fiktiv karakter og partimedlem i actionrollespillet i videospillet Star Wars: Knights of the Old Republic fra 2003, utviklet av BioWare og utgitt av LucasArts. En dyktig pilot og dekorert krigshelt i Den galaktiske republikk som tjenestegjorde i Mandalorian Wars, en viktig bakgrunnskonflikt for serien Knights of the Old Republic , og Carth spiller en nøkkelrolle i krigen mellom den Jedi-støttede galaktiske republikken og Sith Forces under Jedi -borgerkrigen avbildet i Knights of the Old Republic og dens oppfølger, Star Wars: Knights of the Old Republic II: The Sith Lords . Han er også et romantisk alternativ for kvinnelige karakterer. Carth fremstår senere som en tilbakevendende birolle i den månedlige serien Star Wars: Knights of the Old Republic som er prequel -tegneserier. Han blir uttrykt av den amerikanske skuespilleren Raphael Sbarge i videospillene.
Carth Onasi: Carth Onasi er en fiktiv karakter og partimedlem i actionrollespillet i videospillet Star Wars: Knights of the Old Republic fra 2003, utviklet av BioWare og utgitt av LucasArts. En dyktig pilot og dekorert krigshelt i Den galaktiske republikk som tjenestegjorde i Mandalorian Wars, en viktig bakgrunnskonflikt for serien Knights of the Old Republic , og Carth spiller en nøkkelrolle i krigen mellom den Jedi-støttede galaktiske republikken og Sith Forces under Jedi -borgerkrigen avbildet i Knights of the Old Republic og dens oppfølger, Star Wars: Knights of the Old Republic II: The Sith Lords . Han er også et romantisk alternativ for kvinnelige karakterer. Carth fremstår senere som en tilbakevendende birolle i den månedlige serien Star Wars: Knights of the Old Republic som er prequel -tegneserier. Han blir uttrykt av den amerikanske skuespilleren Raphael Sbarge i videospillene.
Carth Onasi: Carth Onasi er en fiktiv karakter og partimedlem i actionrollespillet i videospillet Star Wars: Knights of the Old Republic fra 2003, utviklet av BioWare og utgitt av LucasArts. En dyktig pilot og dekorert krigshelt i Den galaktiske republikk som tjenestegjorde i Mandalorian Wars, en viktig bakgrunnskonflikt for serien Knights of the Old Republic , og Carth spiller en nøkkelrolle i krigen mellom den Jedi-støttede galaktiske republikken og Sith Forces under Jedi -borgerkrigen avbildet i Knights of the Old Republic og dens oppfølger, Star Wars: Knights of the Old Republic II: The Sith Lords . Han er også et romantisk alternativ for kvinnelige karakterer. Carth fremstår senere som en tilbakevendende birolle i den månedlige serien Star Wars: Knights of the Old Republic som er prequel -tegneserier. Han blir uttrykt av den amerikanske skuespilleren Raphael Sbarge i videospillene.
Deke DeLoach: Cartha Dekle DeLoach , kjent som Deke DeLoach , var visedirektør for Federal Bureau of Investigation (FBI) i USA. Under stillingen var DeLoach den tredje høyeste tjenestemannen i FBI etter J. Edgar Hoover og Clyde Tolson.
Deke DeLoach: Cartha Dekle DeLoach , kjent som Deke DeLoach , var visedirektør for Federal Bureau of Investigation (FBI) i USA. Under stillingen var DeLoach den tredje høyeste tjenestemannen i FBI etter J. Edgar Hoover og Clyde Tolson.
Deke DeLoach: Cartha Dekle DeLoach , kjent som Deke DeLoach , var visedirektør for Federal Bureau of Investigation (FBI) i USA. Under stillingen var DeLoach den tredje høyeste tjenestemannen i FBI etter J. Edgar Hoover og Clyde Tolson.
Cartha Doyle: Cartha Doyle [ Childress ] er en tidligere infielder som spilte i All-American Girls Professional Baseball League. Oppført på 5 '5 ", 130 lb., slo hun og kastet høyrehendt.
Cartha Queens Park RFC: Cartha Queens Park Rugby Football Club er en rugbyunions side med base i Glasgow, Skottland. Det ble grunnlagt i 1974, etter sammenslåingen av Cartha RFC og Queens Park FP. De spiller hjemmekampene sine på Dumbreck. Herresiden er for tiden i Scottish National League Division One, damesiden er for tiden i Scottish Womens Premiership.
Cartha Queens Park RFC: Cartha Queens Park Rugby Football Club er en rugbyunions side med base i Glasgow, Skottland. Det ble grunnlagt i 1974, etter sammenslåingen av Cartha RFC og Queens Park FP. De spiller hjemmekampene sine på Dumbreck. Herresiden er for tiden i Scottish National League Division One, damesiden er for tiden i Scottish Womens Premiership.
Cartha RFC: Cartha RFC var en Glasgow-basert rugbyunionsklubb fra det tjuende århundre. Klubben fusjonerte med Queens Park FP for å danne Cartha Queens Park i 1974.
Kartago den eldre: Saint Carthage den eldre var en irsk biskop og abbed på 600 -tallet. Hans festdag er 5. mars.
Cárthach Bán Breathnach: Cárthach Bán Breathnach er en irsk skuespiller og kringkaster. Som skuespiller er han kjent for sine roller i TG4 -serien Aifric og den irske såpeoperaen Ros na Rún .
Mo Chutu fra Lismore: Saint Mo Chutu mac Fínaill , også kjent som Mochuda , Carthach eller Carthach den yngre , var abbed i Rahan, County Offaly og senere grunnlegger og første abbed i Lismore, County Waterford. Helgens liv har kommet ned i flere irske og latinske tilbakemeldinger, som ser ut til å stamme fra en latinsk original skrevet på det 11. eller 12. århundre.
Kartade: Carthade er en slekt av møll fra familien Crambidae. Den inneholder bare en art, Carthade caecalis , som finnes i Colombia.
Kartade: Carthade er en slekt av møll fra familien Crambidae. Den inneholder bare en art, Carthade caecalis , som finnes i Colombia.
Carthaea: Carthaea eller Karthaia var en av de fire gamle greske bystatene på øya Ceos i Kykladene. Det lå på den sørøstlige kysten av øya.
Dryandra møll: Dryandra -møllen er en møllart som anses å være det eneste medlemmet av familien Carthaeidae . Dens nærmeste slektninger er Saturniidae, og den ligner mange arter av familien og har fremtredende øyeflekker på alle vinger. Det vanlige navnet er avledet fra Dryandra- busker av slekten Banksia , som larven til denne arten spiser på, og er derfor begrenset til sør-vest for Vest-Australia hvor disse buskene vokser. Andre Grevillea -busker kan også brukes som vertsplanter.
Dryandra møll: Dryandra -møllen er en møllart som anses å være det eneste medlemmet av familien Carthaeidae . Dens nærmeste slektninger er Saturniidae, og den ligner mange arter av familien og har fremtredende øyeflekker på alle vinger. Det vanlige navnet er avledet fra Dryandra- busker av slekten Banksia , som larven til denne arten spiser på, og er derfor begrenset til sør-vest for Vest-Australia hvor disse buskene vokser. Andre Grevillea -busker kan også brukes som vertsplanter.
Kartago: Kartago var hovedstaden i den gamle kartaginske sivilisasjonen, på østsiden av Tunis -sjøen i det som nå er Tunisia. Kartago var en av de viktigste handelshubbene i det gamle Middelhavet og en av de mest velstående byene i den klassiske verden.
Kartago, Arkansas: Kartago er en by i Dallas County, Arkansas, USA. Befolkningen var 343 ved folketellingen i 2010.
Kartago, Arkansas: Kartago er en by i Dallas County, Arkansas, USA. Befolkningen var 343 ved folketellingen i 2010.
Kartago, Cincinnati: Kartago er et boligområde som ligger i Mill Creek -dalen i Cincinnati, Ohio. Den deler en grense med Elmwood Place, Ohio, som sammen med St. Bernard, Ohio, danner en byøy midt i Cincinnati. Befolkningen var 2.733 ved folketellingen i 2010.
Rådene i Kartago: Councils of Carthage var kirkesynoder som ble holdt i løpet av 3., 4. og 5. århundre i byen Kartago i Afrika. De viktigste av disse er beskrevet nedenfor.
Kartago, Illinois: Kartago er en by i Hancock County, Illinois, USA. Befolkningen var 2.605 ved folketellingen i 2010, ned fra 2.725 i 2000. Det er fylkesetet i Hancock County. Kartago er mest kjent for å være stedet for drapet på Joseph Smith, grunnleggeren av Latter Day Saint -bevegelsen i 1844.
Kartago, Indiana: Kartago er en by i Ripley Township, Rush County, Indiana, USA, som ligger langs Big Blue River. Befolkningen var 927 ved folketellingen i 2010.
Kartago, Illinois: Kartago er en by i Hancock County, Illinois, USA. Befolkningen var 2.605 ved folketellingen i 2010, ned fra 2.725 i 2000. Det er fylkesetet i Hancock County. Kartago er mest kjent for å være stedet for drapet på Joseph Smith, grunnleggeren av Latter Day Saint -bevegelsen i 1844.
Kartago, Illinois: Kartago er en by i Hancock County, Illinois, USA. Befolkningen var 2.605 ved folketellingen i 2010, ned fra 2.725 i 2000. Det er fylkesetet i Hancock County. Kartago er mest kjent for å være stedet for drapet på Joseph Smith, grunnleggeren av Latter Day Saint -bevegelsen i 1844.
Kartago, Indiana: Kartago er en by i Ripley Township, Rush County, Indiana, USA, som ligger langs Big Blue River. Befolkningen var 927 ved folketellingen i 2010.
Kartago, Indiana: Kartago er en by i Ripley Township, Rush County, Indiana, USA, som ligger langs Big Blue River. Befolkningen var 927 ved folketellingen i 2010.
Kartago, Kentucky: Kartago er et ikke- inkorporert samfunn i Campbell County, Kentucky, USA. Kartago ligger i nærheten av Kentucky Route 9, 4,0 km vest-nordvest for California.