Carathéodory's theorem (convex hull)

Carathéodorys teorem (konveks skrog): Carathéodorys teorem er et teorem i konveks geometri. Den sier at hvis et punkt x av R d ligger i det konvekse skroget til et sett P , kan x skrives som den konvekse kombinasjonen av maksimalt d + 1 poeng i P. Nemlig er det en delsett P ′ av P som består av d + 1 eller færre punkter slik at x ligger i det konvekse skroget til P ′. Tilsvarende ligger x i et r -simpleks med hjørner i P , hvor . Den minste r som gjør den siste setningen gyldig for hvert x i det konvekse skroget til P er definert som Carathéodorys antall P. Avhengig av egenskapene til P , kan øvre grenser lavere enn den som tilbys av Carathéodorys teorem oppnås. Vær oppmerksom på at P ikke trenger å være konveks i seg selv. En konsekvens av dette er at P ′ alltid kan være ekstrem i P , da ikke-ekstreme punkter kan fjernes fra P uten å endre medlemskapet til x i det konvekse skroget.
Carathéodorys teorem: I matematikk kan Carathéodorys teorem referere til en av en rekke resultater av Constantin Carathéodory: Carathéodorys teorem, om utvidelse av konforme kartlegginger til grensen Carathéodorys teorem, om de konvekse skrogene til sett i det euklidiske rommet Carathéodorys eksistenssetning, om eksistensen av løsninger på vanlige differensialligninger Carathéodorys forlengelsessats, om utvidelsen av et tiltak Borel - Carathéodory teorem, om begrensningen av en kompleks analytisk funksjon Carathéodory - Jacobi - Lie teorem, en generalisering av Darboux teorem i symplektisk topologi Carathéodorys kriterium, en nødvendig og tilstrekkelig betingelse for et målbart sett Carathéodory -kjernesteoremet, et geometrisk kriterium for lokal ensartet konvergens av univalente funksjoner
Ytre mål: I det matematiske målingsteorien er et ytre mål eller et ytre mål en funksjon definert på alle undergrupper av et gitt sett med verdier i de utvidede reelle tallene som tilfredsstiller noen ytterligere tekniske forhold. Teorien om ytre mål ble først introdusert av Constantin Carathéodory for å gi et abstrakt grunnlag for teorien om målbare sett og adskillige additive mål. Carathéodorys arbeid med ytre mål fant mange anvendelser innen måtteoretisk settteori, og ble brukt på en vesentlig måte av Hausdorff for å definere en dimensjonslignende metrisk invariant som nå kalles Hausdorff-dimensjon. Ytre mål er ofte brukt innen geometrisk målteori.
Teoremet Carathéodory – Jacobi – Lie: Teoremet Carathéodory - Jacobi - Lie er et teorem i symplektisk geometri som generaliserer Darboux 'teorem.
Carathéodorys utvidelsessetning: I tiltaksteori sier Carathéodorys utvidelsessetning at ethvert forhåndsmål som er definert på en gitt ring R av delsett av et gitt sett Ω kan utvides til et mål på σ-algebra generert av R , og denne utvidelsen er unik hvis for- mål er σ-endelig. Følgelig kan ethvert forhåndsmål på en ring som inneholder alle intervaller av reelle tall utvides til Borel-algebraen til settet med reelle tall. Dette er et ekstremt kraftig resultat av tiltaksteori, og fører for eksempel til Lebesgue -målet.
Carathis: Carathis er en slekt av møll i familien Erebidae. Slekten ble beskrevet av Augustus Radcliffe Grote i 1866.
Carathis alayorum: Carathis alayorum er en møll av familien Erebidae som først ble beskrevet av Vitor Osmar Becker i 2011. Den finnes på Cuba.
Carathis australis: Carathis australis er en møll av familien Erebidae som først ble beskrevet av Walter Rothschild i 1909. Den finnes i Brasil.
Carathis byblis: Carathis byblis er en møll av familien Erebidae som først ble beskrevet av William Schaus i 1892. Den finnes i Brasil, Costa Rica og Guatemala.
Carathis gortynoides: Carathis gortynoides er en møll av familien Erebidae som først ble beskrevet av Augustus Radcliffe Grote i 1866. Den finnes på Cuba.
Tessella klagesi: Tessella klagesi er en møll i familien Erebidae. Den ble beskrevet av Walter Rothschild i 1909. Den finnes i Brasil, Fransk Guyana og Ecuador.
Carathis byblis: Carathis byblis er en møll av familien Erebidae som først ble beskrevet av William Schaus i 1892. Den finnes i Brasil, Costa Rica og Guatemala.
Aemilia ockendeni: Aemilia ockendeni er en møll av familien Erebidae som først ble beskrevet av Walter Rothschild i 1909. Den finnes i Peru og Bolivia.
Carathis palpalis: Carathis palpalis er en møll av familien Erebidae som først ble beskrevet av Francis Walker i 1855. Den finnes på Jamaica.
Aemilia peropaca: Aemilia peropaca er en møll av familien Erebidae. Den ble beskrevet av Seitz i 1920. Den finnes i Colombia.
Carathis septentrionalis: Carathis septentrionalis er en møll av familien Erebidae som først ble beskrevet av Vitor Osmar Becker i 2011. Den finnes i Costa Rica.
Aemilia tabaconas: Aemilia tabaconas er en møll av familien Erebidae. Den ble beskrevet av James John Joicey og George Talbot i 1916. Den finnes i Peru.
Carathrips: Carathrips er en slekt av thrips i familien Phlaeothripidae.
Constantin Carathéodory: Constantin Carathéodory var en gresk matematiker som tilbrakte mesteparten av sin profesjonelle karriere i Tyskland. Han ga betydelige bidrag til reell og kompleks analyse, beregning av variasjoner og målteori. Han skapte også en aksiomatisk formulering av termodynamikk.
Carathéodorys kriterium: Carathéodorys kriterium er et resultat i tiltaksteori som ble formulert av den greske matematikeren Constantin Carathéodory. Uttalelsen er som følger: La betegne Lebesgue ytre mål på , og la . Deretter er Lebesgue målbar hvis og bare hvis for hver , betegner komplementet til .Legg merke til det er ikke nødvendig for å være et målbart sett.
Carathéodorys eksistenssetning: I matematikk sier Carathéodorys eksistenssetning at en vanlig differensialligning har en løsning under relativt milde forhold. Det er en generalisering av Peanos eksistenssetning. Peanos teorem krever at høyre side av differensialligningen er kontinuerlig, mens Carathéodorys teorem viser at det finnes løsninger for noen diskontinuerlige ligninger. Teoremet er oppkalt etter Constantin Carathéodory.
Carathéodorys utvidelsessetning: I tiltaksteori sier Carathéodorys utvidelsessetning at ethvert forhåndsmål som er definert på en gitt ring R av delsett av et gitt sett Ω kan utvides til et mål på σ-algebra generert av R , og denne utvidelsen er unik hvis for- mål er σ-endelig. Følgelig kan ethvert forhåndsmål på en ring som inneholder alle intervaller av reelle tall utvides til Borel-algebraen til settet med reelle tall. Dette er et ekstremt kraftig resultat av tiltaksteori, og fører for eksempel til Lebesgue -målet.
Carathéodory kjernestilling: I matematikk er Carathéodory -kjerneteoremet et resultat i kompleks analyse og geometrisk funksjonsteori etablert av den greske matematikeren Constantin Carathéodory i 1912. Den ensartede konvergensen på kompakte sett av en sekvens av holomorfe univalente funksjoner, definert på enhetsdisken i det komplekse planet og fiksering 0, kan formuleres rent geometrisk når det gjelder den begrensende oppførselen til bildene av funksjonene. Kjernens teorem har bred anvendelse i teorien om univalente funksjoner og gir spesielt det geometriske grunnlaget for Loewner differensialligning.
Nevanlinnas kriterium: I matematikk karakteriserer Nevanlinnas kriterium i kompleks analyse, påvist i 1920 av den finske matematikeren Rolf Nevanlinna, holomorfe univalente funksjoner på enhetsdisken som er stjernelignende. Nevanlinna brukte dette kriteriet for å bevise Bieberbach -gjetningen for stjerneaktige univalente funksjoner
Ytre mål: I det matematiske målingsteorien er et ytre mål eller et ytre mål en funksjon definert på alle undergrupper av et gitt sett med verdier i de utvidede reelle tallene som tilfredsstiller noen ytterligere tekniske forhold. Teorien om ytre mål ble først introdusert av Constantin Carathéodory for å gi et abstrakt grunnlag for teorien om målbare sett og adskillige additive mål. Carathéodorys arbeid med ytre mål fant mange anvendelser innen måtteoretisk settteori, og ble brukt på en vesentlig måte av Hausdorff for å definere en dimensjonslignende metrisk invariant som nå kalles Hausdorff-dimensjon. Ytre mål er ofte brukt innen geometrisk målteori.
Carathéodorys teorem: I matematikk kan Carathéodorys teorem referere til en av en rekke resultater av Constantin Carathéodory: Carathéodorys teorem, om utvidelse av konforme kartlegginger til grensen Carathéodorys teorem, om de konvekse skrogene til sett i det euklidiske rommet Carathéodorys eksistenssetning, om eksistensen av løsninger på vanlige differensialligninger Carathéodorys forlengelsessats, om utvidelsen av et tiltak Borel - Carathéodory teorem, om begrensningen av en kompleks analytisk funksjon Carathéodory - Jacobi - Lie teorem, en generalisering av Darboux teorem i symplektisk topologi Carathéodorys kriterium, en nødvendig og tilstrekkelig betingelse for et målbart sett Carathéodory -kjernesteoremet, et geometrisk kriterium for lokal ensartet konvergens av univalente funksjoner
Carathéodorys teorem (konform kartlegging): I matematikk er Carathéodorys teorem et teorem i kompleks analyse, oppkalt etter Constantin Carathéodory, som utvider Riemann -kartleggingssetningen. Teoremet, som først ble bevist i 1913, sier at den konforme kartleggingen som sender enhetsdisken til regionen i det komplekse planet avgrenset av en Jordan -kurve, strekker seg kontinuerlig til en homeomorfisme fra enhetssirkelen inn på Jordan -kurven. Resultatet er et av Carathéodorys resultater på beste ender og grenseadferd for univalente holomorfe funksjoner.
Carathéodorys teorem (konveks skrog): Carathéodorys teorem er et teorem i konveks geometri. Den sier at hvis et punkt x av R d ligger i det konvekse skroget til et sett P , kan x skrives som den konvekse kombinasjonen av maksimalt d + 1 poeng i P. Nemlig er det en delsett P ′ av P som består av d + 1 eller færre punkter slik at x ligger i det konvekse skroget til P ′. Tilsvarende ligger x i et r -simpleks med hjørner i P , hvor . Den minste r som gjør den siste setningen gyldig for hvert x i det konvekse skroget til P er definert som Carathéodorys antall P. Avhengig av egenskapene til P , kan øvre grenser lavere enn den som tilbys av Carathéodorys teorem oppnås. Vær oppmerksom på at P ikke trenger å være konveks i seg selv. En konsekvens av dette er at P ′ alltid kan være ekstrem i P , da ikke-ekstreme punkter kan fjernes fra P uten å endre medlemskapet til x i det konvekse skroget.
Carathéodorys teorem: I matematikk kan Carathéodorys teorem referere til en av en rekke resultater av Constantin Carathéodory: Carathéodorys teorem, om utvidelse av konforme kartlegginger til grensen Carathéodorys teorem, om de konvekse skrogene til sett i det euklidiske rommet Carathéodorys eksistenssetning, om eksistensen av løsninger på vanlige differensialligninger Carathéodorys forlengelsessats, om utvidelsen av et tiltak Borel - Carathéodory teorem, om begrensningen av en kompleks analytisk funksjon Carathéodory - Jacobi - Lie teorem, en generalisering av Darboux teorem i symplektisk topologi Carathéodorys kriterium, en nødvendig og tilstrekkelig betingelse for et målbart sett Carathéodory -kjernesteoremet, et geometrisk kriterium for lokal ensartet konvergens av univalente funksjoner
Ytre mål: I det matematiske målingsteorien er et ytre mål eller et ytre mål en funksjon definert på alle undergrupper av et gitt sett med verdier i de utvidede reelle tallene som tilfredsstiller noen ytterligere tekniske forhold. Teorien om ytre mål ble først introdusert av Constantin Carathéodory for å gi et abstrakt grunnlag for teorien om målbare sett og adskillige additive mål. Carathéodorys arbeid med ytre mål fant mange anvendelser innen måtteoretisk settteori, og ble brukt på en vesentlig måte av Hausdorff for å definere en dimensjonslignende metrisk invariant som nå kalles Hausdorff-dimensjon. Ytre mål er ofte brukt innen geometrisk målteori.
Teoremet Carathéodory – Jacobi – Lie: Teoremet Carathéodory - Jacobi - Lie er et teorem i symplektisk geometri som generaliserer Darboux 'teorem.
Ytre mål: I det matematiske målingsteorien er et ytre mål eller et ytre mål en funksjon definert på alle undergrupper av et gitt sett med verdier i de utvidede reelle tallene som tilfredsstiller noen ytterligere tekniske forhold. Teorien om ytre mål ble først introdusert av Constantin Carathéodory for å gi et abstrakt grunnlag for teorien om målbare sett og adskillige additive mål. Carathéodorys arbeid med ytre mål fant mange anvendelser innen måtteoretisk settteori, og ble brukt på en vesentlig måte av Hausdorff for å definere en dimensjonslignende metrisk invariant som nå kalles Hausdorff-dimensjon. Ytre mål er ofte brukt innen geometrisk målteori.
Carathéodory formodning: I differensialgeometri er Carathéodory -antagelsen en matematisk formodning tilskrevet Constantin Carathéodory av Hans Ludwig Hamburger i en økt i Berlin Mathematical Society i 1924. Carathéodory publiserte et papir om et beslektet emne, men forpliktet seg aldri til å skrive. I, John Edensor Littlewood nevner Conjecture og Hamburger's bidrag som et eksempel på en matematisk påstand som er lett å si, men vanskelig å bevise. Dirk Struik beskriver i den formelle analogien til Conjecture with the Four Vertex Theorem for plane curves. Moderne referanser til formodningen er problemlisten til Shing-Tung Yau, bøkene til Marcel Berger, så vel som bøkene.
Carathéodory formodning: I differensialgeometri er Carathéodory -antagelsen en matematisk formodning tilskrevet Constantin Carathéodory av Hans Ludwig Hamburger i en økt i Berlin Mathematical Society i 1924. Carathéodory publiserte et papir om et beslektet emne, men forpliktet seg aldri til å skrive. I, John Edensor Littlewood nevner Conjecture og Hamburger's bidrag som et eksempel på en matematisk påstand som er lett å si, men vanskelig å bevise. Dirk Struik beskriver i den formelle analogien til Conjecture with the Four Vertex Theorem for plane curves. Moderne referanser til formodningen er problemlisten til Shing-Tung Yau, bøkene til Marcel Berger, så vel som bøkene.
Carathéodorys eksistenssetning: I matematikk sier Carathéodorys eksistenssetning at en vanlig differensialligning har en løsning under relativt milde forhold. Det er en generalisering av Peanos eksistenssetning. Peanos teorem krever at høyre side av differensialligningen er kontinuerlig, mens Carathéodorys teorem viser at det finnes løsninger for noen diskontinuerlige ligninger. Teoremet er oppkalt etter Constantin Carathéodory.
Carathéodorys utvidelsessetning: I tiltaksteori sier Carathéodorys utvidelsessetning at ethvert forhåndsmål som er definert på en gitt ring R av delsett av et gitt sett Ω kan utvides til et mål på σ-algebra generert av R , og denne utvidelsen er unik hvis for- mål er σ-endelig. Følgelig kan ethvert forhåndsmål på en ring som inneholder alle intervaller av reelle tall utvides til Borel-algebraen til settet med reelle tall. Dette er et ekstremt kraftig resultat av tiltaksteori, og fører for eksempel til Lebesgue -målet.
Carathéodory kjernestilling: I matematikk er Carathéodory -kjerneteoremet et resultat i kompleks analyse og geometrisk funksjonsteori etablert av den greske matematikeren Constantin Carathéodory i 1912. Den ensartede konvergensen på kompakte sett av en sekvens av holomorfe univalente funksjoner, definert på enhetsdisken i det komplekse planet og fiksering 0, kan formuleres rent geometrisk når det gjelder den begrensende oppførselen til bildene av funksjonene. Kjernens teorem har bred anvendelse i teorien om univalente funksjoner og gir spesielt det geometriske grunnlaget for Loewner differensialligning.
Ytre mål: I det matematiske målingsteorien er et ytre mål eller et ytre mål en funksjon definert på alle undergrupper av et gitt sett med verdier i de utvidede reelle tallene som tilfredsstiller noen ytterligere tekniske forhold. Teorien om ytre mål ble først introdusert av Constantin Carathéodory for å gi et abstrakt grunnlag for teorien om målbare sett og adskillige additive mål. Carathéodorys arbeid med ytre mål fant mange anvendelser innen måtteoretisk settteori, og ble brukt på en vesentlig måte av Hausdorff for å definere en dimensjonslignende metrisk invariant som nå kalles Hausdorff-dimensjon. Ytre mål er ofte brukt innen geometrisk målteori.
Carathéodory metrisk: I matematikk er Carathéodory -metrikken en metrikk definert på den åpne enhetsballen i et komplekst Banach -rom som har mange lignende egenskaper som Poincaré -metriken for hyperbolsk geometri. Det er oppkalt etter den greske matematikeren Constantin Carathéodory.
Carathéodorys teorem: I matematikk kan Carathéodorys teorem referere til en av en rekke resultater av Constantin Carathéodory: Carathéodorys teorem, om utvidelse av konforme kartlegginger til grensen Carathéodorys teorem, om de konvekse skrogene til sett i det euklidiske rommet Carathéodorys eksistenssetning, om eksistensen av løsninger på vanlige differensialligninger Carathéodorys forlengelsessats, om utvidelsen av et tiltak Borel - Carathéodory teorem, om begrensningen av en kompleks analytisk funksjon Carathéodory - Jacobi - Lie teorem, en generalisering av Darboux teorem i symplektisk topologi Carathéodorys kriterium, en nødvendig og tilstrekkelig betingelse for et målbart sett Carathéodory -kjernesteoremet, et geometrisk kriterium for lokal ensartet konvergens av univalente funksjoner
Carathéodorys teorem (konform kartlegging): I matematikk er Carathéodorys teorem et teorem i kompleks analyse, oppkalt etter Constantin Carathéodory, som utvider Riemann -kartleggingssetningen. Teoremet, som først ble bevist i 1913, sier at den konforme kartleggingen som sender enhetsdisken til regionen i det komplekse planet avgrenset av en Jordan -kurve, strekker seg kontinuerlig til en homeomorfisme fra enhetssirkelen inn på Jordan -kurven. Resultatet er et av Carathéodorys resultater på beste ender og grenseadferd for univalente holomorfe funksjoner.
Carathéodorys teorem (konveks skrog): Carathéodorys teorem er et teorem i konveks geometri. Den sier at hvis et punkt x av R d ligger i det konvekse skroget til et sett P , kan x skrives som den konvekse kombinasjonen av maksimalt d + 1 poeng i P. Nemlig er det en delsett P ′ av P som består av d + 1 eller færre punkter slik at x ligger i det konvekse skroget til P ′. Tilsvarende ligger x i et r -simpleks med hjørner i P , hvor . Den minste r som gjør den siste setningen gyldig for hvert x i det konvekse skroget til P er definert som Carathéodorys antall P. Avhengig av egenskapene til P , kan øvre grenser lavere enn den som tilbys av Carathéodorys teorem oppnås. Vær oppmerksom på at P ikke trenger å være konveks i seg selv. En konsekvens av dette er at P ′ alltid kan være ekstrem i P , da ikke-ekstreme punkter kan fjernes fra P uten å endre medlemskapet til x i det konvekse skroget.
Carathéodorys teorem: I matematikk kan Carathéodorys teorem referere til en av en rekke resultater av Constantin Carathéodory: Carathéodorys teorem, om utvidelse av konforme kartlegginger til grensen Carathéodorys teorem, om de konvekse skrogene til sett i det euklidiske rommet Carathéodorys eksistenssetning, om eksistensen av løsninger på vanlige differensialligninger Carathéodorys forlengelsessats, om utvidelsen av et tiltak Borel - Carathéodory teorem, om begrensningen av en kompleks analytisk funksjon Carathéodory - Jacobi - Lie teorem, en generalisering av Darboux teorem i symplektisk topologi Carathéodorys kriterium, en nødvendig og tilstrekkelig betingelse for et målbart sett Carathéodory -kjernesteoremet, et geometrisk kriterium for lokal ensartet konvergens av univalente funksjoner
Ytre mål: I det matematiske målingsteorien er et ytre mål eller et ytre mål en funksjon definert på alle undergrupper av et gitt sett med verdier i de utvidede reelle tallene som tilfredsstiller noen ytterligere tekniske forhold. Teorien om ytre mål ble først introdusert av Constantin Carathéodory for å gi et abstrakt grunnlag for teorien om målbare sett og adskillige additive mål. Carathéodorys arbeid med ytre mål fant mange anvendelser innen måtteoretisk settteori, og ble brukt på en vesentlig måte av Hausdorff for å definere en dimensjonslignende metrisk invariant som nå kalles Hausdorff-dimensjon. Ytre mål er ofte brukt innen geometrisk målteori.
Teoremet Carathéodory – Jacobi – Lie: Teoremet Carathéodory - Jacobi - Lie er et teorem i symplektisk geometri som generaliserer Darboux 'teorem.
Vanlig halspulsåren: I anatomi er venstre og høyre vanlige halspulsårer ( halspulsårer ) arterier som forsyner hodet og nakken med oksygenrikt blod; de deler seg i nakken for å danne de ytre og indre halspulsårene.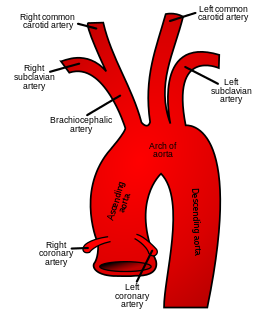
Caratinga: Caratinga er en kommune i østlige Minas Gerais delstat, Brasil. Befolkningen i 2020 var 92 603 innbyggere og det totale arealet til kommunen var 1 251 km 2 . Høyden er 578 meter over havet, med maksimal høyde på 1.516 m i Serra do Rio Preto og 330 m ved munningen av Córrego Boachá.
Feliciano Miguel Abdala Private Natural Heritage Reserve: Feliciano Miguel Abdala Private Natural Heritage Reserve , tidligere Fazenda Montes Claros og deretter Caratinga Biological Station , er et privateid beskyttet område for bærekraftig bruk i delstaten Minas Gerais, Brasil. Den inneholder et eksempel på Atlantic Forest biom. Reservatet er hjemsted for sjeldne buffy-head marmosets og til en av de siste ville populasjonene av nordlige muriqui ullete edderkoppaper.
Cărătnău: Cărătnău kan referere til flere enheter i Romania: Cărătnău de Jos og Cărătnău de Sus, landsbyer i Săruleşti kommune, Buzău County Cărătnău -elven
Pecineaga (elv): Pecineaga eller Peceneaga er en venstre sideelv til elven Slănic i Romania. Den renner ut i Slănic i Vintilă Vodă. Dens lengde er 14 km (8.7 mi) og dens bassenget størrelse er 58 km 2 (22 kvm mi). Følgende landsbyer ligger langs elven Pecineaga, fra kilde til munn: Băltăgari, Sările, Sărulești, Cărătnău de Jos og Vintilă Vodă.
Sărulești, Buzău: Sărulești er en kommune i Buzău County, Muntenia, Romania. Den består av syv landsbyer: Cărătnău de Jos, Cărătnău de Sus, Goicelu, Sările-Cătun, Sărulești, Valea Largă-Sărulești og Valea Stânei.
Sărulești, Buzău: Sărulești er en kommune i Buzău County, Muntenia, Romania. Den består av syv landsbyer: Cărătnău de Jos, Cărătnău de Sus, Goicelu, Sările-Cătun, Sărulești, Valea Largă-Sărulești og Valea Stânei.
Caratoola rekreasjonspark: Caratoola Recreation Park er et beskyttet område i den australske delstaten Sør -Australia, lokalisert i Haslam, omtrent 0,5 kilometer nord for byen Haslam og omtrent 35 kilometer nord for byen Streaky Bay.
Keratosis pilaris: Keratosis pilaris er en vanlig, autosomal-dominerende, genetisk tilstand i hudens hårsekk preget av utseende av muligens kløende, små, gåse-lignende støt, med varierende grad av rødhet eller betennelse. Det vises oftest på yttersidene av overarmene, lårene, ansiktet, ryggen og baken; KP kan også forekomme på hendene og på toppen av bena, sidene eller en hvilken som helst kroppsdel ​​bortsett fra hårløs (hårløs) hud. Ofte kan lesjonene vises i ansiktet, noe som kan forveksles med akne.
Keratosis pilaris: Keratosis pilaris er en vanlig, autosomal-dominerende, genetisk tilstand i hudens hårsekk preget av utseende av muligens kløende, små, gåse-lignende støt, med varierende grad av rødhet eller betennelse. Det vises oftest på yttersidene av overarmene, lårene, ansiktet, ryggen og baken; KP kan også forekomme på hendene og på toppen av bena, sidene eller en hvilken som helst kroppsdel ​​bortsett fra hårløs (hårløs) hud. Ofte kan lesjonene vises i ansiktet, noe som kan forveksles med akne.
Karat: Carat , karat , karet eller karot kan referere til:
Caratti: Caratti er et italiensk etternavn. Kjente personer med etternavnet inkluderer: Cristiano Caratti, italiensk tennisspiller Aaron Caratti, australsk racerfører
Aaron Caratti: Aaron Caratti er en australsk racerfører. Han gikk videre fra karting til Australian Formula Ford Championship før han ble uteksaminert til Australian Formula 3 -serien hvor han ble mester i 2005. Siden har han konkurrert med moderat suksess i sportsbiler.
Carattino: Carattino er et italiensk etternavn. Kjente personer med etternavnet inkluderer: Antonio Carattino, italiensk sjømann Domenico Carattino (1920–2004), italiensk sjømann Giuseppe Carattino (1919–2014), italiensk sjømann
Carattino: Carattino er et italiensk etternavn. Kjente personer med etternavnet inkluderer: Antonio Carattino, italiensk sjømann Domenico Carattino (1920–2004), italiensk sjømann Giuseppe Carattino (1919–2014), italiensk sjømann
Francesco Carattoli: Francesco Carattoli var en italiensk bassbuffo , eller sanger for opera buffa.
Caratunk, Maine: Caratunk er en by i Somerset County, Maine, USA. Befolkningen var 69 ved folketellingen i 2010.
Caratunk, Maine: Caratunk er en by i Somerset County, Maine, USA. Befolkningen var 69 ved folketellingen i 2010.
Caratunk, Maine: Caratunk er en by i Somerset County, Maine, USA. Befolkningen var 69 ved folketellingen i 2010.
Caratunk Falls arkeologiske distrikt: Caratunk Falls arkeologiske distrikt er et kompleks av forhistoriske og historiske arkeologiske steder i Solon, Maine -området. Først identifisert på 1960 -tallet som arkeologisk signifikant, ble stedet kartlagt av statlige arkeologer på begynnelsen av 1980 -tallet. På den tiden var det det største komplekset av arkeologisk betydning i Maine, som omfattet en periode med menneskelig aktivitet fra den arkaiske til den europeiske kontaktperioden. Det 6 mål store området ble oppført i National Register of Historic Places i 1986.
Caratuva -elven: Caratuva -elven er en elv i Paraná -staten i Sør -Brasil . Det er en sideelv til Cantú -elven.
Carau: Carau er en myte, kjent i nordøstlige argentinske fabler.
Carauari: Carauari er en kommune i den brasilianske delstaten Amazonas. Befolkningen var 28 508 (2020) og området er 25 767 km².
Carauari flyplass: Carauari flyplass er flyplassen som betjener Carauari, Brasil.
Caraúbas: Caraúbas er en kommune i delstaten Paraíba i den nordøstlige regionen i Brasil.
Caraúbas, Rio Grande do Norte: Caraúbas er en kommune i delstaten Rio Grande do Norte i den nordøstlige regionen i Brasil.
Caraúbas do Piauí: Caraúbas do Piauí er en kommune i delstaten Piauí i den nordøstlige regionen i Brasil.
Carausius: Marcus Aurelius Mausaeus Carausius var en militær sjef for Romerriket på 300 -tallet. Han var en menapianer fra belgisk Gallia, som overtok makten i 286, under Carausian -opprøret, og erklærte seg selv som keiser i Storbritannia og Nord -Gallia. Han gjorde dette bare 13 år etter at Gallic Empire of the Batavian Postumus ble avsluttet i 273. Han hadde makten i syv år, og formet navnet "Nordens keiser" for seg selv, før han ble myrdet av finansministeren Allectus.
Prosopis kuntzei: Prosopis kuntzei er en søramerikansk belgfulle treslag som lever i de vestligste Gran Chaco -skogene som dekker områder i Argentina, Bolivia og Paraguay, hvor den fungerer som en naturlig komponent. Det har også vært i stand til å kolonisere sabanas i nærheten. Det blir ofte referert til som itín, palo mataco, carandá eller barba de tigre. Det er tilpasset tørt klima, men kan også overleve oversvømmet bakke i lang tid.
Prosopis kuntzei: Prosopis kuntzei er en søramerikansk belgfulle treslag som lever i de vestligste Gran Chaco -skogene som dekker områder i Argentina, Bolivia og Paraguay, hvor den fungerer som en naturlig komponent. Det har også vært i stand til å kolonisere sabanas i nærheten. Det blir ofte referert til som itín, palo mataco, carandá eller barba de tigre. Det er tilpasset tørt klima, men kan også overleve oversvømmet bakke i lang tid.
Prosopis kuntzei: Prosopis kuntzei er en søramerikansk belgfulle treslag som lever i de vestligste Gran Chaco -skogene som dekker områder i Argentina, Bolivia og Paraguay, hvor den fungerer som en naturlig komponent. Det har også vært i stand til å kolonisere sabanas i nærheten. Det blir ofte referert til som itín, palo mataco, carandá eller barba de tigre. Det er tilpasset tørt klima, men kan også overleve oversvømmet bakke i lang tid.
Prosopis kuntzei: Prosopis kuntzei er en søramerikansk belgfulle treslag som lever i de vestligste Gran Chaco -skogene som dekker områder i Argentina, Bolivia og Paraguay, hvor den fungerer som en naturlig komponent. Det har også vært i stand til å kolonisere sabanas i nærheten. Det blir ofte referert til som itín, palo mataco, carandá eller barba de tigre. Det er tilpasset tørt klima, men kan også overleve oversvømmet bakke i lang tid.
Caraula: Caraula er en kommune i Dolj County, Oltenia, Romania med en befolkning på 2560 mennesker. Den består av en enkelt landsby, Caraula.
Caraula: Caraula er en kommune i Dolj County, Oltenia, Romania med en befolkning på 2560 mennesker. Den består av en enkelt landsby, Caraula.
Caraula (elv): Caraula er en venstre sideelv til elven Suceava. Kilden er lokalisert i Chernivtsi Raion, Chernivtsi Oblast, Ukraina. Elven krysser deretter grensen til Romania og slutter seg til Suceava nær landsbyen Vicovu de Sus. I Romania er lengden 4 km (2,5 mi) og bassengets størrelse er 4 km 2 (1,5 kvadrat mi).
Caraula (elv): Caraula er en venstre sideelv til elven Suceava. Kilden er lokalisert i Chernivtsi Raion, Chernivtsi Oblast, Ukraina. Elven krysser deretter grensen til Romania og slutter seg til Suceava nær landsbyen Vicovu de Sus. I Romania er lengden 4 km (2,5 mi) og bassengets størrelse er 4 km 2 (1,5 kvadrat mi).
Caraulun -elven: Caraulun -elven er en elv i Øst -Timor . Det er grensen mellom Ainaro -distriktet og Manufahi -distriktet og renner sørover inn i Timorhavet.
Caraun Reid: Caraun Reid er en amerikansk fotball defensiv takling som er en gratis agent. Han ble draftet av Detroit Lions i den femte runden av NFL Draft 2014. Han spilte college -fotball på Princeton. Han har også vært medlem av San Diego Chargers, Washington Redskins, Indianapolis Colts og Dallas Cowboys.
Carrauntoohil: Carrauntoohil eller Carrauntoohill er det høyeste fjellet på øya Irland på 1038,6 meter. Det er på Iveragh -halvøya i Reeks -distriktet i County Kerry, nær sentrum av Irlands høyeste fjellkjede, MacGillycuddy's Reeks. Carrauntoohil består hovedsakelig av sandstein, hvis isdannelse ga karakteristiske trekk på fjellet, for eksempel Eagle's Nest corrie og noen dype sluker og skarpe arêtes i øst- og nordøstlige ansikter som er populære blant fjell- og vinterklatrere.
Carrauntoohil: Carrauntoohil eller Carrauntoohill er det høyeste fjellet på øya Irland på 1038,6 meter. Det er på Iveragh -halvøya i Reeks -distriktet i County Kerry, nær sentrum av Irlands høyeste fjellkjede, MacGillycuddy's Reeks. Carrauntoohil består hovedsakelig av sandstein, hvis isdannelse ga karakteristiske trekk på fjellet, for eksempel Eagle's Nest corrie og noen dype sluker og skarpe arêtes i øst- og nordøstlige ansikter som er populære blant fjell- og vinterklatrere.
Carrauntoohil: Carrauntoohil eller Carrauntoohill er det høyeste fjellet på øya Irland på 1038,6 meter. Det er på Iveragh -halvøya i Reeks -distriktet i County Kerry, nær sentrum av Irlands høyeste fjellkjede, MacGillycuddy's Reeks. Carrauntoohil består hovedsakelig av sandstein, hvis isdannelse ga karakteristiske trekk på fjellet, for eksempel Eagle's Nest corrie og noen dype sluker og skarpe arêtes i øst- og nordøstlige ansikter som er populære blant fjell- og vinterklatrere.
Carrauntoohil: Carrauntoohil eller Carrauntoohill er det høyeste fjellet på øya Irland på 1038,6 meter. Det er på Iveragh -halvøya i Reeks -distriktet i County Kerry, nær sentrum av Irlands høyeste fjellkjede, MacGillycuddy's Reeks. Carrauntoohil består hovedsakelig av sandstein, hvis isdannelse ga karakteristiske trekk på fjellet, for eksempel Eagle's Nest corrie og noen dype sluker og skarpe arêtes i øst- og nordøstlige ansikter som er populære blant fjell- og vinterklatrere.
Carrauntoohil: Carrauntoohil eller Carrauntoohill er det høyeste fjellet på øya Irland på 1038,6 meter. Det er på Iveragh -halvøya i Reeks -distriktet i County Kerry, nær sentrum av Irlands høyeste fjellkjede, MacGillycuddy's Reeks. Carrauntoohil består hovedsakelig av sandstein, hvis isdannelse ga karakteristiske trekk på fjellet, for eksempel Eagle's Nest corrie og noen dype sluker og skarpe arêtes i øst- og nordøstlige ansikter som er populære blant fjell- og vinterklatrere.
Carrauntoohil: Carrauntoohil eller Carrauntoohill er det høyeste fjellet på øya Irland på 1038,6 meter. Det er på Iveragh -halvøya i Reeks -distriktet i County Kerry, nær sentrum av Irlands høyeste fjellkjede, MacGillycuddy's Reeks. Carrauntoohil består hovedsakelig av sandstein, hvis isdannelse ga karakteristiske trekk på fjellet, for eksempel Eagle's Nest corrie og noen dype sluker og skarpe arêtes i øst- og nordøstlige ansikter som er populære blant fjell- og vinterklatrere.
Carrauntoohil: Carrauntoohil eller Carrauntoohill er det høyeste fjellet på øya Irland på 1038,6 meter. Det er på Iveragh -halvøya i Reeks -distriktet i County Kerry, nær sentrum av Irlands høyeste fjellkjede, MacGillycuddy's Reeks. Carrauntoohil består hovedsakelig av sandstein, hvis isdannelse ga karakteristiske trekk på fjellet, for eksempel Eagle's Nest corrie og noen dype sluker og skarpe arêtes i øst- og nordøstlige ansikter som er populære blant fjell- og vinterklatrere.
Carrauntoohil: Carrauntoohil eller Carrauntoohill er det høyeste fjellet på øya Irland på 1038,6 meter. Det er på Iveragh -halvøya i Reeks -distriktet i County Kerry, nær sentrum av Irlands høyeste fjellkjede, MacGillycuddy's Reeks. Carrauntoohil består hovedsakelig av sandstein, hvis isdannelse ga karakteristiske trekk på fjellet, for eksempel Eagle's Nest corrie og noen dype sluker og skarpe arêtes i øst- og nordøstlige ansikter som er populære blant fjell- og vinterklatrere.
Caraunus: Saint Caraunus av Chartres var en kristen misjonær fra 1. eller 5. århundre i Gallia som ble myrdet av røvere. Hans festdag er 28. mai.
Karaurín-tepui: Karaurín-tepui , også stavet Caraurín , er en tepui fra den østlige Tepuis-kjeden i Bolívar-staten, Venezuela. Den har en maksimal høyde på rundt 2500 meter over havet. Toppmøtet platået er dekket av buskete vegetasjon og har et areal på 1,88 km 2 (0,73 kvm mi). Foten av tepui er dekket av skog. Karaurín-tepui ligger like sør for det mye større Ilú-Tramen-massivet.
Karaurín-tepui: Karaurín-tepui , også stavet Caraurín , er en tepui fra den østlige Tepuis-kjeden i Bolívar-staten, Venezuela. Den har en maksimal høyde på rundt 2500 meter over havet. Toppmøtet platået er dekket av buskete vegetasjon og har et areal på 1,88 km 2 (0,73 kvm mi). Foten av tepui er dekket av skog. Karaurín-tepui ligger like sør for det mye større Ilú-Tramen-massivet.
Karaurín-tepui: Karaurín-tepui , også stavet Caraurín , er en tepui fra den østlige Tepuis-kjeden i Bolívar-staten, Venezuela. Den har en maksimal høyde på rundt 2500 meter over havet. Toppmøtet platået er dekket av buskete vegetasjon og har et areal på 1,88 km 2 (0,73 kvm mi). Foten av tepui er dekket av skog. Karaurín-tepui ligger like sør for det mye større Ilú-Tramen-massivet.
Karaurín-tepui: Karaurín-tepui , også stavet Caraurín , er en tepui fra den østlige Tepuis-kjeden i Bolívar-staten, Venezuela. Den har en maksimal høyde på rundt 2500 meter over havet. Toppmøtet platået er dekket av buskete vegetasjon og har et areal på 1,88 km 2 (0,73 kvm mi). Foten av tepui er dekket av skog. Karaurín-tepui ligger like sør for det mye større Ilú-Tramen-massivet.
Karaurín-tepui: Karaurín-tepui , også stavet Caraurín , er en tepui fra den østlige Tepuis-kjeden i Bolívar-staten, Venezuela. Den har en maksimal høyde på rundt 2500 meter over havet. Toppmøtet platået er dekket av buskete vegetasjon og har et areal på 1,88 km 2 (0,73 kvm mi). Foten av tepui er dekket av skog. Karaurín-tepui ligger like sør for det mye større Ilú-Tramen-massivet.
Karausisk opprør: Carausian -opprøret (286–296 e.Kr.) var en episode i romersk historie, der en romersk sjøkommandør, Carausius, erklærte seg selv som keiser over Storbritannia og Nord -Gallia. Hans galliske territorier ble gjenerobret av den vestlige keiseren Constantius Chlorus i 293, hvoretter Carausius ble myrdet av hans underordnede Allectus. Storbritannia ble gjenvunnet av Constantius og hans underordnede Asclepiodotus i 296.
Karausisk opprør: Carausian -opprøret (286–296 e.Kr.) var en episode i romersk historie, der en romersk sjøkommandør, Carausius, erklærte seg selv som keiser over Storbritannia og Nord -Gallia. Hans galliske territorier ble gjenerobret av den vestlige keiseren Constantius Chlorus i 293, hvoretter Carausius ble myrdet av hans underordnede Allectus. Storbritannia ble gjenvunnet av Constantius og hans underordnede Asclepiodotus i 296.
Carausius: Marcus Aurelius Mausaeus Carausius var en militær sjef for Romerriket på 300 -tallet. Han var en menapianer fra belgisk Gallia, som overtok makten i 286, under Carausian -opprøret, og erklærte seg selv som keiser i Storbritannia og Nord -Gallia. Han gjorde dette bare 13 år etter at Gallic Empire of the Batavian Postumus ble avsluttet i 273. Han hadde makten i syv år, og formet navnet "Nordens keiser" for seg selv, før han ble myrdet av finansministeren Allectus.
Carausius (insekt): Carausius er en slekt av stammen Lonchodini, i rekkefølgen Phasmatodea. Slekten er på mange måter typisk for Phasmatodea ved at alle arter er kvistlignende i utseende. Disse artene er partenogenetiske.
Carausius (insekt): Carausius er en slekt av stammen Lonchodini, i rekkefølgen Phasmatodea. Slekten er på mange måter typisk for Phasmatodea ved at alle arter er kvistlignende i utseende. Disse artene er partenogenetiske.
Carausius II: Carausius II er navnet gitt av historikere til en mulig keiserlig tilnærming i det romerske Storbritannia mellom årene 354 og 358. Mynter dukker opp i løpet av denne perioden med navnet som er det samme som en tidligere britisk usurperkeiser, Carausius.
Carausius morosus: Carausius morosus er en art av Phasmatodea (phasmid) som ofte holdes som kjæledyr av skoler og enkeltpersoner. Kulturaksjer stammer fra en samling fra Tamil Nadu, India. Som de fleste Phasmatodea er C. morosus nattlige. Kulturbestandene er parthenogenetiske hunner som kan reprodusere seg uten parring. Det er ingen rapporter om menn, selv om gynandromorfer noen ganger blir oppdrettet i fangenskap.
Carausius proximus: Carausius proximus er en art av fasmider.
Caravaca de la Cruz: Caravaca de la Cruz , ofte forkortet til Caravaca , er en by og kommune i det sørøstlige Spania i regionen Murcia, nær venstre bredd av elven Argos, en sideelv til Segura. Det er hovedstaden i den nordvestlige regionen Murcia. Den har en befolkning på 26 449 fra og med 2010. I 1900 hadde den 15 846 innbyggere.
Caravaca CF: Caravaca Club de Fútbol var et spansk fotballag med base i Caravaca de la Cruz, i Murcia -regionen. Grunnlagt i 1969 og oppløst i 2011, og holdt hjemmekamper på Estadio Antonio Martínez El Morao , med en kapasitet på 2000 tilskuere.
Caravaca de la Cruz: Caravaca de la Cruz , ofte forkortet til Caravaca , er en by og kommune i det sørøstlige Spania i regionen Murcia, nær venstre bredd av elven Argos, en sideelv til Segura. Det er hovedstaden i den nordvestlige regionen Murcia. Den har en befolkning på 26 449 fra og med 2010. I 1900 hadde den 15 846 innbyggere.
Caravaca de la Cruz: Caravaca de la Cruz , ofte forkortet til Caravaca , er en by og kommune i det sørøstlige Spania i regionen Murcia, nær venstre bredd av elven Argos, en sideelv til Segura. Det er hovedstaden i den nordvestlige regionen Murcia. Den har en befolkning på 26 449 fra og med 2010. I 1900 hadde den 15 846 innbyggere.
Caravaggio: Michelangelo Merisi da Caravaggio , kjent som Caravaggio , var en italiensk maler aktiv i Roma det meste av sitt kunstneriske liv. I løpet av de fire siste årene av livet flyttet han mellom Napoli, Malta og Sicilia til han døde. Maleriene hans har blitt karakterisert av kunstkritikere som å kombinere en realistisk observasjon av menneskelig tilstand, både fysisk og følelsesmessig, med en dramatisk bruk av belysning, som hadde en formativ innflytelse på barokkmaleriet.
Caravaggisti: Caravaggisti var stilistiske tilhengere av den italienske barokkmaleren Caravaggio fra slutten av 1500-tallet. Hans innflytelse på den nye barokkstilen som til slutt kom fra manismen var dyp. Caravaggio etablerte aldri et verksted som de fleste andre malere gjorde, og hadde dermed ingen skole for å spre teknikkene hans. Han la heller aldri frem sin underliggende filosofiske tilnærming til kunst, den psykologiske realismen som bare kan utledes av hans gjenlevende arbeid. Men det kan sees direkte eller indirekte i arbeidet til Rubens, Jusepe de Ribera, Bernini og Rembrandt. Berømt mens han levde, ble Caravaggio selv glemt nesten umiddelbart etter hans død. Mange av maleriene hans ble tilskrevet tilhengere av ham, for eksempel The Taking of Christ , som ble tilskrevet den nederlandske maleren Gerrit van Honthorst til 1990. Det var først på 1900 -tallet at hans betydning for utviklingen av vestlig kunst ble gjenoppdaget. På 1920 -tallet plasserte Roberto Longhi ham igjen i den europeiske tradisjonen: "Ribera, Vermeer, La Tour og Rembrandt kunne aldri ha eksistert uten ham. Og kunsten til Delacroix, Courbet og Manet hadde vært helt annerledes". Den innflytelsesrike Bernard Berenson uttalte: "Med unntak av Michelangelo hadde ingen annen italiensk maler så stor innflytelse."
Caravaggio: Michelangelo Merisi da Caravaggio , kjent som Caravaggio , var en italiensk maler aktiv i Roma det meste av sitt kunstneriske liv. I løpet av de fire siste årene av livet flyttet han mellom Napoli, Malta og Sicilia til han døde. Maleriene hans har blitt karakterisert av kunstkritikere som å kombinere en realistisk observasjon av menneskelig tilstand, både fysisk og følelsesmessig, med en dramatisk bruk av belysning, som hadde en formativ innflytelse på barokkmaleriet.
Caravaggio: Michelangelo Merisi da Caravaggio , kjent som Caravaggio , var en italiensk maler aktiv i Roma det meste av sitt kunstneriske liv. I løpet av de fire siste årene av livet flyttet han mellom Napoli, Malta og Sicilia til han døde. Maleriene hans har blitt karakterisert av kunstkritikere som å kombinere en realistisk observasjon av menneskelig tilstand, både fysisk og følelsesmessig, med en dramatisk bruk av belysning, som hadde en formativ innflytelse på barokkmaleriet.
Caravaggio: Michelangelo Merisi da Caravaggio , kjent som Caravaggio , var en italiensk maler aktiv i Roma det meste av sitt kunstneriske liv. I løpet av de fire siste årene av livet flyttet han mellom Napoli, Malta og Sicilia til han døde. Maleriene hans har blitt karakterisert av kunstkritikere som å kombinere en realistisk observasjon av menneskelig tilstand, både fysisk og følelsesmessig, med en dramatisk bruk av belysning, som hadde en formativ innflytelse på barokkmaleriet.
Caravaggio, Lombardia: Caravaggio er en by og kommune i provinsen Bergamo, i Lombardia, Italia, 40 kilometer øst for Milano.
Caravaggio, Lombardia: Caravaggio er en by og kommune i provinsen Bergamo, i Lombardia, Italia, 40 kilometer øst for Milano.
Liste over malerier av Caravaggio: Følgende er en liste over malerier av den italienske kunstneren Caravaggio , oppført kronologisk.
Caravaggio, il pittore maledetto: Caravaggio, il pittore maledetto er en italiensk historisk dramafilm fra 1941 regissert av Goffredo Alessandrini og med Amedeo Nazzari, Clara Calamai og Lamberto Picasso i hovedrollen. Nazzari fremstiller maleren Caravaggio som et egensinnig geni. Det var en av hans favorittskjermroller.
Caravaggio, il pittore maledetto: Caravaggio, il pittore maledetto er en italiensk historisk dramafilm fra 1941 regissert av Goffredo Alessandrini og med Amedeo Nazzari, Clara Calamai og Lamberto Picasso i hovedrollen. Nazzari fremstiller maleren Caravaggio som et egensinnig geni. Det var en av hans favorittskjermroller.
Caravaggio (film fra 1986): Caravaggio er en britisk historisk dramafilm fra 1986 regissert av Derek Jarman. Filmen er en fiksjonalisert gjenfortelling om livet til barokkmaleren Michelangelo Merisi da Caravaggio. Det er filmdebuten til Tilda Swinton og Sean Bean.
Caravaggio (miniserie): Caravaggio er en italiensk TV -miniserie fra 2007 regissert av Angelo Longoni. Filmen er basert på hendelser fra den barokke maleren Michelangelo Merisi da Caravaggio fra det virkelige liv.