Bessel function

Bessel-funksjon: Bessel-funksjoner , først definert av matematikeren Daniel Bernoulli og deretter generalisert av Friedrich Bessel, er kanoniske løsninger y ( x ) av Bessels differensialligning
Bessel-funksjon: Bessel-funksjoner , først definert av matematikeren Daniel Bernoulli og deretter generalisert av Friedrich Bessel, er kanoniske løsninger y ( x ) av Bessels differensialligning
Johann Franz Bessel: Johann Franz Bessel var en tysk benediktinsk abbed og historiker.
Richard Bessel: Richard Bessel er professor i det tjuende århundre historie ved University of York og medlem av redaksjonene for German History and History Today . Han er spesialist i den sosiale og politiske historien til det moderne Tyskland, ettervirkningen av de to verdenskrigene og politiets historie.
Bessel – Clifford-funksjon: I matematisk analyse er funksjonen Bessel – Clifford , oppkalt etter Friedrich Bessel og William Kingdon Clifford, en hel funksjon av to komplekse variabler som kan brukes til å gi en alternativ utvikling av teorien om Bessel-funksjoner. Hvis
Bessel bjelke: En Bessel-stråle er en bølge hvis amplitude er beskrevet av en Bessel-funksjon av den første typen. Elektromagnetiske, akustiske, gravitasjons- og materiebølger kan alle være i form av Bessel-bjelker. En ekte Bessel-bjelke er ikke-diffraktiv. Dette betyr at når den forplanter seg, blir den ikke diffundert og spredt; Dette er i motsetning til den vanlige oppførselen til lys, som sprer seg etter å ha blitt fokusert ned til et lite sted. Bessel-bjelker er også selvhelbredende , noe som betyr at bjelken kan være delvis blokkert på ett punkt, men vil omformes på et punkt lenger ned på bjelkeaksen.
Bessel – Maitland-funksjon: I matematikk er funksjonen Bessel – Maitland , eller Wright generalisert Bessel-funksjon , en generalisering av Bessel-funksjonen, introdusert av Edward Maitland Wright (1934). Ordet "Maitland" i navnet på funksjonen ser ut til å være et resultat av å forvirre Edward Maitland Wrights mellom- og etternavn. Det er gitt av
Bessel-Oberrealschule: Bessel-Oberrealschule var en Oberrealschule i Königsberg, Tyskland.
Bessel (krater): Bessel er et lite måneskollkrater som ligger i den sørlige halvdelen av Mare Serenitatis. Krateret ble oppkalt etter den tyske astronomen Friedrich Wilhelm Bessel i 1935. Til tross for den lille størrelsen er dette det største krateret som ligger helt innenfor hoppa. Det ligger nord-nordøst for krateret Menelaus.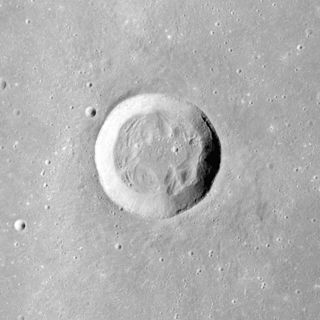
Bessel: Bessel kan referere til: Bessel stråle Bessel ellipsoid Bessel-funksjon i matematikk Bessels ulikhet i matematikk Bessels rettelse i statistikk. Bessel-filter, et lineært filter som ofte brukes i lydovergangssystemer Bessel Fjord, NE Grønland Bessel Fjord, NW Grønland Bessel (krater), et lite månekrater Bessel transform, også kjent som Fourier-Bessel transform eller Hankel transform Bessel-vindu, i signalbehandling Besselian-dato, se epoke (astronomi) #Besselian-år MV Bessel , et tysk handelsskip i tjeneste 1928–45, sistnevnte for Kriegsmarine
Bessel ellipsoid: Bessel-ellipsoiden er en viktig geodesi-referanse-ellipsoid. Den brukes for tiden av flere land til sine nasjonale geodetiske undersøkelser, men vil bli erstattet i de neste tiårene av moderne ellipsoider fra satellittgeodesi.
Bessel Fjord: Bessel Fjord er en fjord nordøst på Grønland. Administrativt tilhører det NE Greenland National Park-området.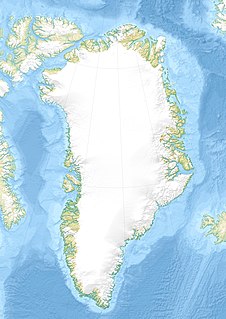
Bessel Fjord, NW Grønland: Bessel Fjord , også kjent som Bessels Bay , er en fjord nordvest på Grønland. Administrativt tilhører det kommunen Avannaata.
Bessel-funksjon: Bessel-funksjoner , først definert av matematikeren Daniel Bernoulli og deretter generalisert av Friedrich Bessel, er kanoniske løsninger y ( x ) av Bessels differensialligning
Bessel Kok: Bessel Kok er en nederlandsk forretningsmann og sjakkarrangør som bor i Praha. Han har hatt topplederstillinger i telekommunikasjonsselskaper i Belgia (Belgacom) og i Tsjekkia. Han var også president for det belgiske baserte bankkommunikasjonsselskapet SWIFT og ansvarlig for SWIFTs sponsing av flere store internasjonale sjakkarrangementer.
Bessel-funksjon: Bessel-funksjoner , først definert av matematikeren Daniel Bernoulli og deretter generalisert av Friedrich Bessel, er kanoniske løsninger y ( x ) av Bessels differensialligning
Bessel bjelke: En Bessel-stråle er en bølge hvis amplitude er beskrevet av en Bessel-funksjon av den første typen. Elektromagnetiske, akustiske, gravitasjons- og materiebølger kan alle være i form av Bessel-bjelker. En ekte Bessel-bjelke er ikke-diffraktiv. Dette betyr at når den forplanter seg, blir den ikke diffundert og spredt; Dette er i motsetning til den vanlige oppførselen til lys, som sprer seg etter å ha blitt fokusert ned til et lite sted. Bessel-bjelker er også selvhelbredende , noe som betyr at bjelken kan være delvis blokkert på ett punkt, men vil omformes på et punkt lenger ned på bjelkeaksen.
Bessels rettelse: I statistikken er Bessels korreksjon bruk av n - 1 i stedet for n i formelen for prøvevariansen og standardavviket, hvor n er antall observasjoner i et utvalg. Denne metoden korrigerer skjevheten i estimeringen av populasjonsvariansen. Det korrigerer også skjevheten i estimeringen av populasjonsstandardavviket. Imidlertid øker korreksjonen ofte den gjennomsnittlige kvadratiske feilen i disse estimatene. Denne teknikken er oppkalt etter Friedrich Bessel.
Bessel filter: I elektronikk og signalbehandling er et Bessel-filter en type analog lineært filter med en maksimal flat gruppe / faseforsinkelse, som bevarer bølgeformen til filtrerte signaler i passbåndet. Bessel-filtre brukes ofte i crossover-lydsystemer.
Bessel-funksjon: Bessel-funksjoner , først definert av matematikeren Daniel Bernoulli og deretter generalisert av Friedrich Bessel, er kanoniske løsninger y ( x ) av Bessels differensialligning
Bessel ellipsoid: Bessel-ellipsoiden er en viktig geodesi-referanse-ellipsoid. Den brukes for tiden av flere land til sine nasjonale geodetiske undersøkelser, men vil bli erstattet i de neste tiårene av moderne ellipsoider fra satellittgeodesi.
Bessel-funksjon: Bessel-funksjoner , først definert av matematikeren Daniel Bernoulli og deretter generalisert av Friedrich Bessel, er kanoniske løsninger y ( x ) av Bessels differensialligning
Bessel filter: I elektronikk og signalbehandling er et Bessel-filter en type analog lineært filter med en maksimal flat gruppe / faseforsinkelse, som bevarer bølgeformen til filtrerte signaler i passbåndet. Bessel-filtre brukes ofte i crossover-lydsystemer.
Bessel-funksjon: Bessel-funksjoner , først definert av matematikeren Daniel Bernoulli og deretter generalisert av Friedrich Bessel, er kanoniske løsninger y ( x ) av Bessels differensialligning
Varians-gammafordeling: Varians-gammadistribusjon , generalisert Laplace-fordeling eller Bessel-funksjonsfordeling er en kontinuerlig sannsynlighetsfordeling som er definert som den normale varians-middelblandingen der blandingstettheten er gammadistribusjonen. Fordelingens haler avtar saktere enn normalfordelingen. Det er derfor hensiktsmessig å modellere fenomener der numerisk store verdier er mer sannsynlige enn det som er tilfelle for normalfordelingen. Eksempler er avkastning fra finansielle eiendeler og turbulente vindhastigheter. Distribusjonen ble introdusert i finanslitteraturen av Madan og Seneta. Variansen-gammadistribusjonene danner en underklasse av de generaliserte hyperbolldistribusjonene.
Bessel-funksjon: Bessel-funksjoner , først definert av matematikeren Daniel Bernoulli og deretter generalisert av Friedrich Bessel, er kanoniske løsninger y ( x ) av Bessels differensialligning
Bessel-funksjon: Bessel-funksjoner , først definert av matematikeren Daniel Bernoulli og deretter generalisert av Friedrich Bessel, er kanoniske løsninger y ( x ) av Bessels differensialligning
Bessel-funksjon: Bessel-funksjoner , først definert av matematikeren Daniel Bernoulli og deretter generalisert av Friedrich Bessel, er kanoniske løsninger y ( x ) av Bessels differensialligning
Bessel-funksjon: Bessel-funksjoner , først definert av matematikeren Daniel Bernoulli og deretter generalisert av Friedrich Bessel, er kanoniske løsninger y ( x ) av Bessels differensialligning
Bessel-funksjon: Bessel-funksjoner , først definert av matematikeren Daniel Bernoulli og deretter generalisert av Friedrich Bessel, er kanoniske løsninger y ( x ) av Bessels differensialligning
Bessel-funksjon: Bessel-funksjoner , først definert av matematikeren Daniel Bernoulli og deretter generalisert av Friedrich Bessel, er kanoniske løsninger y ( x ) av Bessels differensialligning
Bessel-funksjon: Bessel-funksjoner , først definert av matematikeren Daniel Bernoulli og deretter generalisert av Friedrich Bessel, er kanoniske løsninger y ( x ) av Bessels differensialligning
Bessel-funksjon: Bessel-funksjoner , først definert av matematikeren Daniel Bernoulli og deretter generalisert av Friedrich Bessel, er kanoniske løsninger y ( x ) av Bessels differensialligning
Bessels ulikhet: I matematikk, spesielt funksjonell analyse, er Bessels ulikhet en uttalelse om koeffisientene til et element i et Hilbert-rom med hensyn til en ortonormal sekvens. Ulikheten ble avledet av FW Bessel i 1828.
Bessel-funksjon: Bessel-funksjoner , først definert av matematikeren Daniel Bernoulli og deretter generalisert av Friedrich Bessel, er kanoniske løsninger y ( x ) av Bessels differensialligning
Bessel-funksjon: Bessel-funksjoner , først definert av matematikeren Daniel Bernoulli og deretter generalisert av Friedrich Bessel, er kanoniske løsninger y ( x ) av Bessels differensialligning
Bessel polynomer: I matematikk er Bessel-polynomene en ortogonal sekvens av polynomer. Det finnes en rekke forskjellige, men nært beslektede definisjoner. Definisjonen favorisert av matematikere er gitt av serien
Bessel polynomer: I matematikk er Bessel-polynomene en ortogonal sekvens av polynomer. Det finnes en rekke forskjellige, men nært beslektede definisjoner. Definisjonen favorisert av matematikere er gitt av serien
Bessel potensiale: I matematikk er Bessel-potensialet et potensial som ligner på Riesz-potensialet, men med bedre forfallegenskaper ved uendelig.
Bessel potensiale: I matematikk er Bessel-potensialet et potensial som ligner på Riesz-potensialet, men med bedre forfallegenskaper ved uendelig.
Bessel potensiale: I matematikk er Bessel-potensialet et potensial som ligner på Riesz-potensialet, men med bedre forfallegenskaper ved uendelig.
Bessel-prosess: I matematikk er en Bessel-prosess , oppkalt etter Friedrich Bessel, en type stokastisk prosess.
Bessel-prosess: I matematikk er en Bessel-prosess , oppkalt etter Friedrich Bessel, en type stokastisk prosess.
Hankel transform: I matematikk uttrykker Hankel-transformasjonen en gitt funksjon f ( r ) som den vektede summen av et uendelig antall Bessel-funksjoner av den første typen J ν ( kr ) . Bessel-funksjonene i summen er alle av samme rekkefølge ν, men avviker i en skaleringsfaktor k langs r- aksen. Den nødvendige koeffisienten F v av hver Bessel-funksjon i summen, som en funksjon av skaleringsfaktoren k utgjør den transformerte funksjonen. Hankel-transformasjonen er en integrert transformasjon og ble først utviklet av matematikeren Hermann Hankel. Det er også kjent som Fourier – Bessel-transformasjonen. Akkurat som Fourier-transformasjonen for et uendelig intervall er relatert til Fourier-serien over et endelig intervall, slik er Hankel-transformasjonen over et uendelig intervall relatert til Fourier – Bessel-serien over et endelig intervall.
Bessel van der Kolk: Bessel van der Kolk er psykiater, forfatter, forsker og pedagog basert i Boston, USA. Siden 1970-tallet har forskningen hans vært innen posttraumatisk stress. Han er forfatter av The New York Times bestselger , The Body Keeps the Score . Van der Kolk fungerte som tidligere president for International Society for Traumatic stress Studies og tidligere meddirektør for National Child Traumatic Stress Network. Han er professor i psykiatri ved Boston University School of Medicine og president for Trauma Research Foundation i Brookline, Massachusetts.
Vindusfunksjon: I signalbehandling og statistikk er en vindusfunksjon en matematisk funksjon som er nullverdi utenfor noe valgt intervall, vanligvis symmetrisk rundt midten av intervallet, vanligvis nær et maksimum i midten, og vanligvis avtar fra midten. Matematisk, når en annen funksjon eller bølgeform / datasekvens "multipliseres" med en vindusfunksjon, er produktet også nullverdi utenfor intervallet: alt som er igjen er den delen de overlapper, "utsikten gjennom vinduet". Tilsvarende, og i praksis, blir datasegmentet i vinduet først isolert, og deretter bare at dataene multipliseres med vindusfunksjonens verdier. Dermed er avsmalning, ikke segmentering, hovedformålet med vindusfunksjoner.
Phyllis Reynolds Naylor: Phyllis Reynolds Naylor er en amerikansk forfatter som er mest kjent for fiksjon for barn og unge voksne. Naylor er best kjent for barneromankvartetten Shiloh og for hennes "Alice" -bokserie, en av de mest utfordrede bøkene i det siste tiåret.
Se rundt deg: Look Around You er en britisk tv-komedieserie utviklet og skrevet av Robert Popper og Peter Serafinowicz, og fortalt i den første serien av Nigel Lambert. Den første serien på åtte 10-minutters shorts ble vist i 2002, og den andre serien på seks 30-minutters episoder i 2005, begge på BBC Two. Den første serien av Look Around You ble nominert til en BAFTA-pris i 2003.
Se rundt deg: Look Around You er en britisk tv-komedieserie utviklet og skrevet av Robert Popper og Peter Serafinowicz, og fortalt i den første serien av Nigel Lambert. Den første serien på åtte 10-minutters shorts ble vist i 2002, og den andre serien på seks 30-minutters episoder i 2005, begge på BBC Two. Den første serien av Look Around You ble nominert til en BAFTA-pris i 2003.
Besselian elementer: De Besselian-elementene er et sett med verdier som brukes til å beregne og forutsi de lokale omstendighetene for okkulasjoner for en observatør på jorden. Denne metoden brukes spesielt til solformørkelser, men brukes også til okkultasjoner av stjerner eller planeter ved månen og gjennomganger av Venus eller Merkur. I tillegg brukes for måneformørkelser en lignende metode, der skyggen kastes på månen i stedet for jorden.
Besselian elementer: De Besselian-elementene er et sett med verdier som brukes til å beregne og forutsi de lokale omstendighetene for okkulasjoner for en observatør på jorden. Denne metoden brukes spesielt til solformørkelser, men brukes også til okkultasjoner av stjerner eller planeter ved månen og gjennomganger av Venus eller Merkur. I tillegg brukes for måneformørkelser en lignende metode, der skyggen kastes på månen i stedet for jorden.
Epoke (astronomi): I astronomi er en epoke eller referansepoke et øyeblikk som brukes som referansepunkt for en tidsvarierende astronomisk størrelse. Det er nyttig for himmelkoordinatene eller banelementene til en himmellegeme, da de er utsatt for forstyrrelser og varierer med tiden. Disse tidsvarierende astronomiske størrelsene kan for eksempel inkludere en kropps gjennomsnittlig lengdegrad eller gjennomsnittlig anomali, knutepunktet for bane i forhold til et referanseplan, retning av apogee eller aphelion av bane, eller størrelsen på majoren sin bane.
Epoke (astronomi): I astronomi er en epoke eller referansepoke et øyeblikk som brukes som referansepunkt for en tidsvarierende astronomisk størrelse. Det er nyttig for himmelkoordinatene eller banelementene til en himmellegeme, da de er utsatt for forstyrrelser og varierer med tiden. Disse tidsvarierende astronomiske størrelsene kan for eksempel inkludere en kropps gjennomsnittlig lengdegrad eller gjennomsnittlig anomali, knutepunktet for bane i forhold til et referanseplan, retning av apogee eller aphelion av bane, eller størrelsen på majoren sin bane.
Besseling: Besseling er et etternavn. Kjente personer med etternavnet inkluderer: Alice Besseling (1944–2014), nederlandsk politiker JF Besseling (1928–2015), nederlandsk professor Peter Besseling, australsk politiker Wil Besseling, nederlandsk golfspiller
Peter Besseling: Peter Edward Besseling er en australsk politiker. Besseling var ordfører i Port Macquarie-Hastings Council, fra 8. september 2012 til 8. mai 2017, som uavhengig. Besseling fungerte som medlem for Port Macquarie mellom 2008 og 2011. Besseling er nå daglig leder i Birdon Pty Ltd.
Paul Besselink: Paul Besselink er en nederlandsk gjerder. Han konkurrerte i team épée-arrangementet ved sommer-OL 1988.
Bessell: Bessell er et etternavn. Kjente personer med etternavnet inkluderer: Alfred Bessell-Browne (1877–1947), australske hærens oberst og midlertidig brigadegeneral i første verdenskrig Eric Bessell (1923–1979), australsk politiker Peter Bessell (1921–1985), britisk politiker Ted Bessell (1935–1996), amerikansk TV-skuespiller
Eric Bessell: Eric James Bessell var en australsk politiker. Han ble født i Launceston, Tasmania, og var pastoralist før han tjenestegjorde i den australske hæren som privatperson under andre verdenskrig. Han fungerte som president for Tasmanian Liberal Party i 1966 og 1973. I 1974 ble han valgt til det australske senatet som en liberal senator for Tasmania. Han ble beseiret i 1975 etter å ha blitt degradert til sjette plass på stemmeseddelen for å gi plass til eiendomsmegler Brian Archer og sykepleier Shirley Walters. Bessell døde i 1979.
Peter Bessell: Peter Joseph Bessell var en britisk Venstre-politiker og parlamentsmedlem for Bodmin i Cornwall fra 1964 til 1970.
Bessel-funksjon: Bessel-funksjoner , først definert av matematikeren Daniel Bernoulli og deretter generalisert av Friedrich Bessel, er kanoniske løsninger y ( x ) av Bessels differensialligning
Besselpark: Besselpark er en park i Kreuzberg, Berlin, Tyskland. Skulpturen Tilted Donut Wedge with Two Balls er installert i parken.
Emil Bessels: Emil Bessels var en tysk zoolog, entomolog, lege og arktisk forsker som er mest kjent for sin kontroversielle rolle i den forsøkte, men uredde Polaris- ekspedisjonen til Nordpolen i 1871. Omfattende bevis peker sterkt på Bessels som den mest sannsynlige mistenkte i ekspedisjonens sjef, den amerikanske utforskeren Charles Francis Hall, døde av arsenforgiftning.
Bessels Green: Bessels Green er en landsby som nå er innlemmet i det bebygde området Sevenoaks i Kent, England. Det ligger i den nordvestlige utkanten av Sevenoaks, i sogn Chevening. Ved folketellingen i 2011 ble landsbybefolkningen inkludert i det sivile menigheten Sundridge med Ide Hill. Den travle stamruten på A25 går gjennom sentrum av landsbyen.
Besselsleigh: Besselsleigh eller Bessels Leigh er en landsby og sivil sogne om 4 + 1/2 miles (7 km) sør-vest for Oxford. Besselsleigh var en del av Berkshire til grenseendringene i 1974 overførte den til Oxfordshire.
Parklands Campus: Parklands Campus var en uavhengig spesialskole for gutter og jenter i alderen 11 til 19 i nærheten av Abingdon, Oxfordshire, England, som ikke ble opprettholdt. Den ble stengt i 2016 og har siden denne datoen vært ledig. I 2018 har Millgate Homes foreslått en ny utvikling for landet.
Bessel-funksjon: Bessel-funksjoner , først definert av matematikeren Daniel Bernoulli og deretter generalisert av Friedrich Bessel, er kanoniske løsninger y ( x ) av Bessels differensialligning
Bessel-funksjon: Bessel-funksjoner , først definert av matematikeren Daniel Bernoulli og deretter generalisert av Friedrich Bessel, er kanoniske løsninger y ( x ) av Bessels differensialligning
Bessels ulikhet: I matematikk, spesielt funksjonell analyse, er Bessels ulikhet en uttalelse om koeffisientene til et element i et Hilbert-rom med hensyn til en ortonormal sekvens. Ulikheten ble avledet av FW Bessel i 1828.
Besselsbreen: Besselsbreen er en bre på Barentsøya, Svalbard. Det er den største utløpet av Barentsjøkulen, og når ned til sjøen i nordøstlig retning, vest for punktet Kapp Bessels. Breen er oppkalt etter den tyske arktiske utforskeren Emil Bessels.
Besselsleigh: Besselsleigh eller Bessels Leigh er en landsby og sivil sogne om 4 + 1/2 miles (7 km) sør-vest for Oxford. Besselsleigh var en del av Berkshire til grenseendringene i 1974 overførte den til Oxfordshire.
Besselsleigh: Besselsleigh eller Bessels Leigh er en landsby og sivil sogne om 4 + 1/2 miles (7 km) sør-vest for Oxford. Besselsleigh var en del av Berkshire til grenseendringene i 1974 overførte den til Oxfordshire.
Besselvassheia: Besselvassheia er et fjell i Frøya kommune i Trøndelag fylke, Norge. Det 76 meter høye fjellet er det høyeste punktet på øya Frøya. Den ligger omtrent 4 kilometer vest for landsbyen Sistranda og omtrent 4 kilometer nordvest for landsbyen Hammarvika.
Bessel – Clifford-funksjon: I matematisk analyse er funksjonen Bessel – Clifford , oppkalt etter Friedrich Bessel og William Kingdon Clifford, en hel funksjon av to komplekse variabler som kan brukes til å gi en alternativ utvikling av teorien om Bessel-funksjoner. Hvis
Bessel – Maitland-funksjon: I matematikk er funksjonen Bessel – Maitland , eller Wright generalisert Bessel-funksjon , en generalisering av Bessel-funksjonen, introdusert av Edward Maitland Wright (1934). Ordet "Maitland" i navnet på funksjonen ser ut til å være et resultat av å forvirre Edward Maitland Wrights mellom- og etternavn. Det er gitt av
Bessels rettelse: I statistikken er Bessels korreksjon bruk av n - 1 i stedet for n i formelen for prøvevariansen og standardavviket, hvor n er antall observasjoner i et utvalg. Denne metoden korrigerer skjevheten i estimeringen av populasjonsvariansen. Det korrigerer også skjevheten i estimeringen av populasjonsstandardavviket. Imidlertid øker korreksjonen ofte den gjennomsnittlige kvadratiske feilen i disse estimatene. Denne teknikken er oppkalt etter Friedrich Bessel.
Bassem Nafti: Bassem Nafti er en tunisisk fotball midtbanespiller.
Bessemer: Bessemer kan referere til:
Bessemer, Alabama: Bessemer er en sørvestlig forstad til Birmingham i Jefferson County, Alabama, USA. Befolkningen var 27 456 ved folketellingen 2010. Det ligger i Birmingham-Hoover, AL Metropolitan Statistical Area, hvor Jefferson County er sentrum. Den utviklet seg raskt som en industriby på slutten av 1800-tallet og tidlig på 1900-tallet. I 2019 ble den kåret til Alabamas "Worst City to Live in" av Wall Street 24/7.
Bessemer, Alabama: Bessemer er en sørvestlig forstad til Birmingham i Jefferson County, Alabama, USA. Befolkningen var 27 456 ved folketellingen 2010. Det ligger i Birmingham-Hoover, AL Metropolitan Statistical Area, hvor Jefferson County er sentrum. Den utviklet seg raskt som en industriby på slutten av 1800-tallet og tidlig på 1900-tallet. I 2019 ble den kåret til Alabamas "Worst City to Live in" av Wall Street 24/7.
Bessemer, Alabama: Bessemer er en sørvestlig forstad til Birmingham i Jefferson County, Alabama, USA. Befolkningen var 27 456 ved folketellingen 2010. Det ligger i Birmingham-Hoover, AL Metropolitan Statistical Area, hvor Jefferson County er sentrum. Den utviklet seg raskt som en industriby på slutten av 1800-tallet og tidlig på 1900-tallet. I 2019 ble den kåret til Alabamas "Worst City to Live in" av Wall Street 24/7.
Anthony Bessemer: Anthony Bessemer var en britisk ingeniør og industri, som tilbrakte store deler av livet sitt i Nederland og Frankrike før han vendte tilbake for å bo i London og Hertfordshire. Hans sønn var Sir Henry Bessemer, oppfinneren av Bessemer-prosessen for stålproduksjon.
Bessemer (Pueblo): Bessemer, Colorado var en by i Colorado som ble innlemmet i 1886. Samfunnet ble oppkalt etter Henry Bessemer, en engelsk oppfinner. Det var en av fire tilstøtende byer som ble avgjort etter Colorado Gold Rush i 1859. Samfunnene Sør-Pueblo, Sentrale Pueblo, Pueblo og Bessemer ble senere slått sammen for å skape den moderne byen Pueblo, Colorado. Bessemer var en uavhengig by til 1894 og var den siste byen som ble med i Pueblo. Det tidligere samfunnet Bessemer blir noen ganger nå referert til som Bessemer-området. Det er også kjent som Bessemer-området. Bessemer-området er hjemsted for både Bessemer Academy og Bessemer park.
Bessemer, Lawrence County, Pennsylvania: Bessemer er en bydel i Lawrence County, Pennsylvania, USA. Befolkningen var 1111 ved folketellingen i 2010.
Bessemer, Michigan: Bessemer er en by i den amerikanske delstaten Michigan. Fra og med folketellingen i 2010 var byens befolkning 1.914. Det er fylkesetet til Gogebic County.
Bessemer, Michigan: Bessemer er en by i den amerikanske delstaten Michigan. Fra og med folketellingen i 2010 var byens befolkning 1.914. Det er fylkesetet til Gogebic County.
Bessemer, Ohio: Bessemer er et ikke-innlemmet samfunn i Athens County, i den amerikanske delstaten Ohio.
Carlow / Mayo: Carlow / Mayo er et township i det nordlige Hastings County i Øst-Ontario, Canada. Det ble dannet i 2001 ved sammenslåing av townships Carlow og Mayo .
Bessemer, Pennsylvania: Bessemer, Pennsylvania kan referere til: Bessemer, North Braddock, Allegheny County, Pennsylvania Bessemer, Lawrence County, Pennsylvania Bessemer, Westmoreland County, Pennsylvania
Bessemer, Pennsylvania: Bessemer, Pennsylvania kan referere til: Bessemer, North Braddock, Allegheny County, Pennsylvania Bessemer, Lawrence County, Pennsylvania Bessemer, Westmoreland County, Pennsylvania
Bessemer, Pennsylvania: Bessemer, Pennsylvania kan referere til: Bessemer, North Braddock, Allegheny County, Pennsylvania Bessemer, Lawrence County, Pennsylvania Bessemer, Westmoreland County, Pennsylvania
Bessemer, Virginia: Bessemer er et ikke-innlemmet samfunn i Botetourt County, Virginia, USA. Det var fødestedet til arbeidsleder Frank Fairfax.
Bessemer, West Virginia: Bessemer er et ikke-innlemmet samfunn på US Route 11 i Berkeley County, West Virginia, USA.
Bessemer, West Virginia: Bessemer er et ikke-innlemmet samfunn på US Route 11 i Berkeley County, West Virginia, USA.
Bessemer, Westmoreland County, Pennsylvania: Bessemer er et befolket sted i Westmoreland County, Pennsylvania, USA med koordinater \ t40.1281278, -79.5550387 innenfor Mount Pleasant, Pennsylvania. En vei med navnet Bessemer Road ligger i nærheten av koordinatene for det befolkede stedet oppført i databasen Geographic Names Information System.
Bessemer prosess: Bessemer-prosessen var den første billige industrielle prosessen for masseproduksjon av stål fra smeltet råjern før utviklingen av den åpne ildstedet. Nøkkelprinsippet er fjerning av urenheter fra jernet ved oksidasjon med luft som blåses gjennom smeltet jern. Oksidasjonen øker også temperaturen på jernmassen og holder den smeltet.
Bessemer prosess: Bessemer-prosessen var den første billige industrielle prosessen for masseproduksjon av stål fra smeltet råjern før utviklingen av den åpne ildstedet. Nøkkelprinsippet er fjerning av urenheter fra jernet ved oksidasjon med luft som blåses gjennom smeltet jern. Oksidasjonen øker også temperaturen på jernmassen og holder den smeltet.
Bessemer (Pueblo): Bessemer, Colorado var en by i Colorado som ble innlemmet i 1886. Samfunnet ble oppkalt etter Henry Bessemer, en engelsk oppfinner. Det var en av fire tilstøtende byer som ble avgjort etter Colorado Gold Rush i 1859. Samfunnene Sør-Pueblo, Sentrale Pueblo, Pueblo og Bessemer ble senere slått sammen for å skape den moderne byen Pueblo, Colorado. Bessemer var en uavhengig by til 1894 og var den siste byen som ble med i Pueblo. Det tidligere samfunnet Bessemer blir noen ganger nå referert til som Bessemer-området. Det er også kjent som Bessemer-området. Bessemer-området er hjemsted for både Bessemer Academy og Bessemer park.
Bessemer og Lake Erie Railroad: Bessemer and Lake Erie Railroad er en klasse II jernbane som opererer i det nordvestlige Pennsylvania og nordøstlige Ohio.
Bessemer og Lake Erie Railroad: Bessemer and Lake Erie Railroad er en klasse II jernbane som opererer i det nordvestlige Pennsylvania og nordøstlige Ohio.
Bessemer & Lake Erie Railroad Bridge: Bessemer & Lake Erie Railroad Bridge er en bindingsverksbro som fører den kanadiske nasjonale jernbanens divisjon Bessemer og Lake Erie Railroad over Allegheny River mellom Pittsburgh forsteder til Plum og Harmar Township, Pennsylvania. I 1897 ble det bygd en enkeltsporsbuk og viadukt på dette nettstedet; i 1918 ble de opprinnelige bryggene doblet i bredden, den nåværende dobbeltsporede strukturen ble bygd ved siden av, og deretter glidet på plass. Den opprinnelige tilnærmingen til nordbukk ble gravlagt i slagg dumpet fra en tilstøtende midlertidig fyllbukk.
Bessemer (Pueblo): Bessemer, Colorado var en by i Colorado som ble innlemmet i 1886. Samfunnet ble oppkalt etter Henry Bessemer, en engelsk oppfinner. Det var en av fire tilstøtende byer som ble avgjort etter Colorado Gold Rush i 1859. Samfunnene Sør-Pueblo, Sentrale Pueblo, Pueblo og Bessemer ble senere slått sammen for å skape den moderne byen Pueblo, Colorado. Bessemer var en uavhengig by til 1894 og var den siste byen som ble med i Pueblo. Det tidligere samfunnet Bessemer blir noen ganger nå referert til som Bessemer-området. Det er også kjent som Bessemer-området. Bessemer-området er hjemsted for både Bessemer Academy og Bessemer park.
Bessemer: Bessemer kan referere til:
Stevens, Shanks & Sons Ltd .: Stevens, Shanks & Sons Ltd. var et støperi av engelsk type som ble dannet i 1933 ved fusjonen av Figgins Foundry med PM Shanks for å danne Stevens, Shanks. En gang etter 1971 opphørte støperiet og alt materiale gikk til St. Brides utskriftsbibliotek.
Bessemer Academy: Bessemer Academy er en privat skole i Bessemer, Alabama. Den ble grunnlagt i 1970 som et segregeringsakademi. Deres atletiske lag får kallenavnet opprørerne etter konfødererte soldater i den amerikanske borgerkrigen. Konkurranse i sport innen Alabama Independent School Association, som ble opprettet av for å gi konkurranse for disse skolene. Som mange akademier for segregering rapporterer de ikke statistikk til NCES.
Bessemer flyplass: Bessemer lufthavn er en byeid offentlig flyplass som ligger tre nautiske mil sørøst for det sentrale forretningsområdet i Bessemer, en by i Jefferson County, Alabama, USA. I henhold til FAAs nasjonale plan for integrerte flyplasssystemer for 2009–2013, er den kategorisert som en avlastningsflyplass for Birmingham-Shuttlesworth internasjonale lufthavn.
Bessemer arkeologiske funnsted: Bessemer Archaeological Site er et forhistorisk indianersted i Botetourt County, Virginia. Området ble først gravd ut i 1977 før Virginia Route 220 ble bygget gjennom området, og igjen i 1987 da veibanen ble utvidet. Den inkluderte brennkammer, bevis på en stor rektangulær bygning, steinredskaper og keramikkflis. Menneskelige gravplasser ble også identifisert, i tillegg til plasseringen av deler av en palisade som sannsynligvis omringet bosetningen.
Bessemer Bend, Wyoming: Bessemer Bend er et folketellingsutpekt sted (CDP) i Natrona County, Wyoming, USA. Det er en del av Casper, Wyoming Metropolitan Statistical Area. Befolkningen var 199 ved folketellingen 2010.
Bessemer Bend, Wyoming: Bessemer Bend er et folketellingsutpekt sted (CDP) i Natrona County, Wyoming, USA. Det er en del av Casper, Wyoming Metropolitan Statistical Area. Befolkningen var 199 ved folketellingen 2010.
DUX Bessemer Bend Bridge: DUX Bessemer Bend Bridge var en Warren gjennom fagverksbro i Bessemer Bend, Wyoming, som bar Natrona County Road CN1-58 over North Platte River. Broen ble bygget fra 1921 til 1922. Da den ble nominert til National Register of Historic Places i 1982, var den en av bare tre Warren gjennom fagverksbroer som var igjen på Wyoming County Highways. I tillegg lå broen på stedet av en historisk elvekryssing på Oregon Trail.
Bessemer City: Bessemer City kan referere til: - Bessemer City, North Carolina SS Bessemer City , et skip ødelagt i nærheten av St. Ives, Cornwall i 1936.
Bessemer City, North Carolina: Bessemer City er en liten forstadsby i Gaston County, North Carolina, USA. Befolkningen er 5.340. Byen ligger omtrent 10 km nordvest for Gastonia og 40 km vest for Charlotte. Det ble avgjort i 1756 og grunnlagt i 1893.
Bessemer City, North Carolina: Bessemer City er en liten forstadsby i Gaston County, North Carolina, USA. Befolkningen er 5.340. Byen ligger omtrent 10 km nordvest for Gastonia og 40 km vest for Charlotte. Det ble avgjort i 1756 og grunnlagt i 1893.
Gaston County skoler: Gaston County Schools er et offentlig skoledistrikt som ligger i Gaston County, North Carolina. Med 31 189 studenter på 55 skoler fra og med studieåret 2012–13, er det det niende største offentlige skoledistriktet i North Carolina.
Bessemer City Downtown Historic District: Bessemer City Downtown Historic District er et nasjonalt historisk distrikt i Bessemer City, Gaston County, North Carolina. Det omfatter 23 bidragende bygninger og 10 bidragskonstruksjoner i Bessemer Citys sentrale forretningsdistrikt. Bygningene ble bygget mellom etter 1896, og inkluderer en- og to-etasjes kommersielle bygninger og to store, viltvoksende tekstilfabrikker. Merkbare bygninger inkluderer: Whetstone Cotton Mills-Huss Manufacturing Company-Algodon Manufacturing Division of Pyramid Mills Southern Cotton Mills-Osage Manufacturing Company Gamble maskinvare Central Drug Store Winn-Dixie dagligvare Shulmans varehus Kincaid servicestasjon og Pontiac-forhandler.
Bessemer videregående skole: Bessemer City High School kan referere til: Bessemer City High School (Alabama) Bessemer City videregående skole
Bessemer City High School (Alabama): Bessemer City High School ( BCHS ) er en fireårig offentlig videregående skole i Bessemer, Alabama. Det er den eneste videregående skolen i Bessemer City School System. Skolefarger er lilla og hvite, og atletiske lag kalles tigrene. BCHS konkurrerer i AHSAA klasse 6A friidrett.
Bessemer City High School (North Carolina): Bessemer City High School er en videregående skole i Gaston County Schools skoledistrikt i Bessemer City, NC. Deltakelsesområdet dekker den sentrale delen av det vestlige Gaston County, og det serverer også den østlige delen av samfunnet Tryon, deler av Nordvest-Gastonia og det omkringliggende landlige området. Sheila Wyont fungerer som rektor. Tom Potter og Melissa Knick er assisterende rektor. Larry Boone fungerer som atletisk leder. Mateskolen er Bessemer City Middle School.
Bessemer videregående skole: Bessemer City High School kan referere til: Bessemer City High School (Alabama) Bessemer City videregående skole
Gaston County skoler: Gaston County Schools er et offentlig skoledistrikt som ligger i Gaston County, North Carolina. Med 31 189 studenter på 55 skoler fra og med studieåret 2012–13, er det det niende største offentlige skoledistriktet i North Carolina.
Bessemer City, North Carolina: Bessemer City er en liten forstadsby i Gaston County, North Carolina, USA. Befolkningen er 5.340. Byen ligger omtrent 10 km nordvest for Gastonia og 40 km vest for Charlotte. Det ble avgjort i 1756 og grunnlagt i 1893.
Gaston County skoler: Gaston County Schools er et offentlig skoledistrikt som ligger i Gaston County, North Carolina. Med 31 189 studenter på 55 skoler fra og med studieåret 2012–13, er det det niende største offentlige skoledistriktet i North Carolina.