Higgs mechanism

Higgs mekanisme: I standardmodellen for partikkelfysikk er Higgs-mekanismen viktig for å forklare genereringsmekanismen for egenskapen "masse" for målebosoner. Uten Higgs-mekanismen vil alle bosoner (en av de to partiklene, den andre er fermioner) bli betraktet som masseløse, men målinger viser at W + , W - og Z 0- bosonene faktisk har relativt store masser på rundt 80 GeV / c 2 . Higgs-feltet løser dette problemet. Den enkleste beskrivelsen av mekanismen legger til et kvantefelt (Higgs-feltet) som gjennomsyrer all plass til standardmodellen. Under noen ekstremt høy temperatur forårsaker feltet spontan symmetri som bryter under interaksjoner. Brudd på symmetri utløser Higgs-mekanismen, og får bosonene den samhandler med til å ha masse. I standardmodellen refererer uttrykket "Higgs-mekanisme" spesifikt til generering av masser for W ± og Z svake målere bosoner gjennom elektrosvak symmetribrudd. Large Hadron Collider på CERN kunngjorde resultater i samsvar med Higgs-partikkelen 14. mars 2013, noe som gjorde det ekstremt sannsynlig at feltet, eller en som det, eksisterte, og forklarte hvordan Higgs-mekanismen foregår i naturen.
Higgs mekanisme: I standardmodellen for partikkelfysikk er Higgs-mekanismen viktig for å forklare genereringsmekanismen for egenskapen "masse" for målebosoner. Uten Higgs-mekanismen vil alle bosoner (en av de to partiklene, den andre er fermioner) bli betraktet som masseløse, men målinger viser at W + , W - og Z 0- bosonene faktisk har relativt store masser på rundt 80 GeV / c 2 . Higgs-feltet løser dette problemet. Den enkleste beskrivelsen av mekanismen legger til et kvantefelt (Higgs-feltet) som gjennomsyrer all plass til standardmodellen. Under noen ekstremt høy temperatur forårsaker feltet spontan symmetri som bryter under interaksjoner. Brudd på symmetri utløser Higgs-mekanismen, og får bosonene den samhandler med til å ha masse. I standardmodellen refererer uttrykket "Higgs-mekanisme" spesifikt til generering av masser for W ± og Z svake målere bosoner gjennom elektrosvak symmetribrudd. Large Hadron Collider på CERN kunngjorde resultater i samsvar med Higgs-partikkelen 14. mars 2013, noe som gjorde det ekstremt sannsynlig at feltet, eller en som det, eksisterte, og forklarte hvordan Higgs-mekanismen foregår i naturen.
Abelsk integral: I matematikk er en abelsk integral , oppkalt etter den norske matematikeren Niels Henrik Abel, en integral i formens komplekse plan
Løgealgebra: I matematikk er en Lie-algebra et vektorrom sammen med en operasjon kalt Lie-braketten , et vekslende bilinært kart , som tilfredsstiller Jacobi-identiteten. Vektorområdet sammen med denne operasjonen er en ikke-assosiativ algebra, noe som betyr at Lie-braketten ikke nødvendigvis er assosiativ.
Abelian Lie-gruppen: I geometri er en abelian Lie-gruppe en Lie-gruppe som er en abelian-gruppe.
Abel polynomer: Abel polynomer i matematikk danne et polynom sekvens, det n-te sikt som har sådan form
Abelianske og tauberske teoremer: I matematikk er abeliske og tauberske teoremer teoremer som gir betingelser for to metoder for å summere divergerende serier for å gi det samme resultatet, oppkalt etter Niels Henrik Abel og Alfred Tauber. De originale eksemplene er Abels teorem som viser at hvis en serie konvergerer til en eller annen grense, så er Abelsummen den samme grensen, og Taubers teorem viser at hvis Abelsummen av en serie eksisterer og koeffisientene er tilstrekkelig små, så konvergerer serien til Abel sum. Mer generelle abeliske og tauberske teoremer gir lignende resultater for mer generelle summeringsmetoder.
Abelsk variasjon: I matematikk, spesielt innen algebraisk geometri, kompleks analyse og algebraisk tallteori, er en abelsk variant en prosjektiv algebraisk variasjon som også er en algebraisk gruppe, dvs. har en gruppelov som kan defineres av vanlige funksjoner. Abelske varianter er samtidig blant de mest studerte objektene innen algebraisk geometri og uunnværlige verktøy for mye forskning på andre emner innen algebraisk geometri og tallteori.
Assosiativ algebra: I matematikk er en assosiativ algebra en algebraisk struktur med kompatible operasjoner av tillegg, multiplikasjon og en skalar multiplikasjon med elementer i et eller annet felt. Tilleggs- og multiplikasjonsoperasjonene sammen gir A strukturen til en ring; tilleggs- og skalar multiplikasjonsoperasjoner gir sammen A strukturen til et vektorrom over K. I denne artikkelen vil vi også bruke begrepet K- algebra for å bety en assosiativ algebra over feltet K. Et standard første eksempel på en K- algebra er en ring av firkantede matriser over et felt K , med vanlig matrisemultiplikasjon.
Abelianske og tauberske teoremer: I matematikk er abeliske og tauberske teoremer teoremer som gir betingelser for to metoder for å summere divergerende serier for å gi det samme resultatet, oppkalt etter Niels Henrik Abel og Alfred Tauber. De originale eksemplene er Abels teorem som viser at hvis en serie konvergerer til en eller annen grense, så er Abelsummen den samme grensen, og Taubers teorem viser at hvis Abelsummen av en serie eksisterer og koeffisientene er tilstrekkelig små, så konvergerer serien til Abel sum. Mer generelle abeliske og tauberske teoremer gir lignende resultater for mer generelle summeringsmetoder.
Abelianske og tauberske teoremer: I matematikk er abeliske og tauberske teoremer teoremer som gir betingelser for to metoder for å summere divergerende serier for å gi det samme resultatet, oppkalt etter Niels Henrik Abel og Alfred Tauber. De originale eksemplene er Abels teorem som viser at hvis en serie konvergerer til en eller annen grense, så er Abelsummen den samme grensen, og Taubers teorem viser at hvis Abelsummen av en serie eksisterer og koeffisientene er tilstrekkelig små, så konvergerer serien til Abel sum. Mer generelle abeliske og tauberske teoremer gir lignende resultater for mer generelle summeringsmetoder.
Abelsk kategori: I matematikk er en abelsk kategori en kategori der morfismer og gjenstander kan legges til og der kjerner og kokkerner eksisterer og har ønskelige egenskaper. Det motiverende prototypiske eksemplet på en abelsk kategori er kategorien abeliske grupper, Ab . Teorien oppsto i et forsøk på å forene flere kohomologiteorier av Alexander Grothendieck og uavhengig i det litt tidligere arbeidet til David Buchsbaum. Abelske kategorier er veldig stabile kategorier; for eksempel er de vanlige og de tilfredsstiller slangelemmaet. Klassen av abelske kategorier er stengt under flere kategoriske konstruksjoner, for eksempel er kategorien av kjedekomplekser i en abelsk kategori, eller kategorien funksjonere fra en liten kategori til en abelsk kategori også abelsk. Disse stabilitetsegenskapene gjør dem uunngåelige i homologisk algebra og utover; teorien har store anvendelser innen algebraisk geometri, kohomologi og ren kategoriteori. Abelske kategorier er oppkalt etter Niels Henrik Abel.
Abelsk kategori: I matematikk er en abelsk kategori en kategori der morfismer og gjenstander kan legges til og der kjerner og kokkerner eksisterer og har ønskelige egenskaper. Det motiverende prototypiske eksemplet på en abelsk kategori er kategorien abeliske grupper, Ab . Teorien oppsto i et forsøk på å forene flere kohomologiteorier av Alexander Grothendieck og uavhengig i det litt tidligere arbeidet til David Buchsbaum. Abelske kategorier er veldig stabile kategorier; for eksempel er de vanlige og de tilfredsstiller slangelemmaet. Klassen av abelske kategorier er stengt under flere kategoriske konstruksjoner, for eksempel er kategorien av kjedekomplekser i en abelsk kategori, eller kategorien funksjonere fra en liten kategori til en abelsk kategori også abelsk. Disse stabilitetsegenskapene gjør dem uunngåelige i homologisk algebra og utover; teorien har store anvendelser innen algebraisk geometri, kohomologi og ren kategoriteori. Abelske kategorier er oppkalt etter Niels Henrik Abel.
Kompleksitetsfunksjon: I informatikk er kompleksitetsfunksjonen til en streng, en endelig eller uendelig sekvens av bokstaver fra et eller annet alfabet, funksjonen som teller antall forskjellige faktorer fra den strengen. Mer generelt teller kompleksitetsfunksjonen til et språk, et sett med endelige ord over et alfabet, antall forskjellige ord med gitt lengde.
Dekningsgruppe: I matematikk er en dekkende gruppe av en topologisk gruppe H et dekkingsrom G av H slik at G er en topologisk gruppe og dekkekartet p : G → H er en kontinuerlig gruppe homomorfisme. Kartet p kalles dekkende homomorfisme . Et ofte forekommende tilfelle er en dobbelt dekkende gruppe , et topologisk dobbelt dekke der H har indeks 2 i G ; eksempler inkluderer spinngrupper, pinnegrupper og metaplektiske grupper.
Differensial av den første typen: I matematikk er differensial av første slag et tradisjonelt begrep som brukes i teoriene om Riemann-overflater og algebraiske kurver, for overalt-vanlige differensial 1-former. Gitt en kompleks manifold M , er en differensial av den første typen therefore derfor den samme tingen som en 1-form som er overalt holomorf; på en algebraisk variant V som ikke er entall, ville det være en global del av den sammenhengende skiven Ω 1 av Kähler-differensialene. I begge tilfeller har definisjonen sin opprinnelse i teorien om abelske integraler.
Abelsk forlengelse: I abstrakt algebra er en abelsk forlengelse en Galois-utvidelse hvis Galois-gruppe er abelsk. Når Galois-gruppen også er syklisk, kalles utvidelsen også en syklisk forlengelse . Går i den andre retningen, kalles en Galois-utvidelse løsbar hvis Galois-gruppen er løsbar, dvs. hvis gruppen kan spaltes i en serie normale utvidelser av en abelsk gruppe.
Abelsk forlengelse: I abstrakt algebra er en abelsk forlengelse en Galois-utvidelse hvis Galois-gruppe er abelsk. Når Galois-gruppen også er syklisk, kalles utvidelsen også en syklisk forlengelse . Går i den andre retningen, kalles en Galois-utvidelse løsbar hvis Galois-gruppen er løsbar, dvs. hvis gruppen kan spaltes i en serie normale utvidelser av en abelsk gruppe.
Abelsk variasjon: I matematikk, spesielt innen algebraisk geometri, kompleks analyse og algebraisk tallteori, er en abelsk variant en prosjektiv algebraisk variasjon som også er en algebraisk gruppe, dvs. har en gruppelov som kan defineres av vanlige funksjoner. Abelske varianter er samtidig blant de mest studerte objektene innen algebraisk geometri og uunnværlige verktøy for mye forskning på andre emner innen algebraisk geometri og tallteori.
Målerteori: I fysikk er en gauge-teori en type feltteori der Lagrangian ikke endres under lokale transformasjoner fra visse Lie-grupper.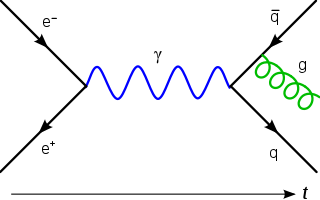
Matematisk vits: En matematisk vits er en form for humor som er avhengig av aspekter av matematikk eller en stereotype matematikere. Humoren kan komme fra et ordspill, eller fra en dobbel betydning av et matematisk begrep, eller fra en lekes misforståelse av et matematisk konsept. Matematiker og forfatter John Allen Paulos beskrev i sin bok Mathematics and Humor flere måter at matematikk, generelt sett på som en tørr, formell aktivitet, overlapper med humor, en løs, ærbødig aktivitet: begge er former for "intellektuelt spill"; begge har "logikk, mønster, regler, struktur"; og begge er "økonomiske og eksplisitte".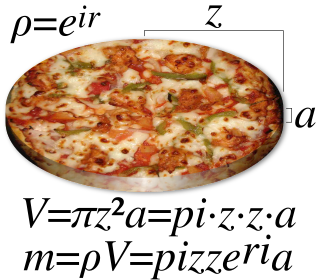
Abelsk gruppe: I matematikk er en abelsk gruppe , også kalt kommutativ gruppe , en gruppe der resultatet av å bruke gruppeoperasjonen på to gruppeelementer ikke avhenger av rekkefølgen de skrives i. Det vil si at gruppedriften er kommutativ. Med tillegg som en operasjon, danner heltallene og de reelle tallene abeliske grupper, og konseptet med en abelisk gruppe kan sees på som en generalisering av disse eksemplene. Abelske grupper er oppkalt etter matematikeren Niels Henrik Abel fra det 19. århundre.
Abelsk gruppe: I matematikk er en abelsk gruppe , også kalt kommutativ gruppe , en gruppe der resultatet av å bruke gruppeoperasjonen på to gruppeelementer ikke avhenger av rekkefølgen de skrives i. Det vil si at gruppedriften er kommutativ. Med tillegg som en operasjon, danner heltallene og de reelle tallene abeliske grupper, og konseptet med en abelisk gruppe kan sees på som en generalisering av disse eksemplene. Abelske grupper er oppkalt etter matematikeren Niels Henrik Abel fra det 19. århundre.
Abelsk integral: I matematikk er en abelsk integral , oppkalt etter den norske matematikeren Niels Henrik Abel, en integral i formens komplekse plan
Lokaliseringsformel for ekvivariant kohomologi: I differensialgeometri sier lokaliseringsformelen : for en ekvivariant lukket ekvivariant differensialform på en orbifold M med en torus handling og for en tilstrekkelig liten i Lie-algebra av torus T ,
Ulike serier: I matematikk er en divergerende serie en uendelig serie som ikke er konvergent, noe som betyr at den uendelige sekvensen av delsummen til serien ikke har en endelig grense.
Monoid: I abstrakt algebra, en gren av matematikken, er en monoid et sett utstyrt med en assosiativ binær operasjon og et identitetselement.
Klassefeltteori: I matematikk er klassefeltteori grenen av algebraisk tallteori som er opptatt av abeliske utvidelser av tallfelt, globale felt med positive karakteristika og lokale felt. Teorien hadde sitt utspring i beviset på kvadratisk gjensidighet av Gauss på slutten av 1700-tallet. Disse ideene ble utviklet i løpet av det neste århundre, og ga opphav til et sett av antagelser av Hilbert som senere ble bevist av Takagi og Artin. Disse antagelsene og deres bevis utgjør hoveddelen av klassefeltteorien.
Idempotent (ringteori): I ringteori er et idempotent element , eller rett og slett et idempotent , av en ring et element a slik at a 2 = a . Det vil si at elementet er idempotent under ringens multiplikasjon. Induktivt da kan man også konkludere med at a = a 2 = a 3 = a 4 = ... = a n for ethvert positivt heltall n . For eksempel er et idempotent element i en matrisering nettopp en idempotent matrise.
Abels sandpæle modell: Den abelske sandpælemodellen , også kjent som Bak – Tang – Wiesenfeld-modellen , var det første oppdagede eksemplet på et dynamisk system som viste selvorganisert kritikk. Den ble introdusert av Per Bak, Chao Tang og Kurt Wiesenfeld i en artikkel fra 1987.
Abels sandpæle modell: Den abelske sandpælemodellen , også kjent som Bak – Tang – Wiesenfeld-modellen , var det første oppdagede eksemplet på et dynamisk system som viste selvorganisert kritikk. Den ble introdusert av Per Bak, Chao Tang og Kurt Wiesenfeld i en artikkel fra 1987.
Abelsk variasjon: I matematikk, spesielt innen algebraisk geometri, kompleks analyse og algebraisk tallteori, er en abelsk variant en prosjektiv algebraisk variasjon som også er en algebraisk gruppe, dvs. har en gruppelov som kan defineres av vanlige funksjoner. Abelske varianter er samtidig blant de mest studerte objektene innen algebraisk geometri og uunnværlige verktøy for mye forskning på andre emner innen algebraisk geometri og tallteori.
Semigroup: I matematikk er en semigruppe en algebraisk struktur som består av et sett sammen med en assosiativ binær operasjon.
Modulskive: I matematikk er en skive O- moduler eller bare en O- modul over et ringet rom en skive F slik at F ( U ) for ethvert åpent delmengde U av X er et O ( U ) -modul og begrensningskartene F ( U ) → F ( V ) er kompatible med begrensningskartene O ( U ) → O ( V ): begrensningen av fs er begrensningen av f ganger den for s for enhver f i O ( U ) og s i F ( U ).
Abelsk gruppe: I matematikk er en abelsk gruppe , også kalt kommutativ gruppe , en gruppe der resultatet av å bruke gruppeoperasjonen på to gruppeelementer ikke avhenger av rekkefølgen de skrives i. Det vil si at gruppedriften er kommutativ. Med tillegg som en operasjon, danner heltallene og de reelle tallene abeliske grupper, og konseptet med en abelisk gruppe kan sees på som en generalisering av disse eksemplene. Abelske grupper er oppkalt etter matematikeren Niels Henrik Abel fra det 19. århundre.
Abels teorem: I matematikk relaterer Abels teorem for kraftserier en grense for en kraftserie til summen av koeffisientene. Den er oppkalt etter norsk matematiker Niels Henrik Abel.
Abelsk overflate: I matematikk er en abelsk overflate 2-dimensjonal abelsk variasjon.
Abelianske og tauberske teoremer: I matematikk er abeliske og tauberske teoremer teoremer som gir betingelser for to metoder for å summere divergerende serier for å gi det samme resultatet, oppkalt etter Niels Henrik Abel og Alfred Tauber. De originale eksemplene er Abels teorem som viser at hvis en serie konvergerer til en eller annen grense, så er Abelsummen den samme grensen, og Taubers teorem viser at hvis Abelsummen av en serie eksisterer og koeffisientene er tilstrekkelig små, så konvergerer serien til Abel sum. Mer generelle abeliske og tauberske teoremer gir lignende resultater for mer generelle summeringsmetoder.
Abelsk variasjon: I matematikk, spesielt innen algebraisk geometri, kompleks analyse og algebraisk tallteori, er en abelsk variant en prosjektiv algebraisk variasjon som også er en algebraisk gruppe, dvs. har en gruppelov som kan defineres av vanlige funksjoner. Abelske varianter er samtidig blant de mest studerte objektene innen algebraisk geometri og uunnværlige verktøy for mye forskning på andre emner innen algebraisk geometri og tallteori.
Abelsk variasjon: I matematikk, spesielt innen algebraisk geometri, kompleks analyse og algebraisk tallteori, er en abelsk variant en prosjektiv algebraisk variasjon som også er en algebraisk gruppe, dvs. har en gruppelov som kan defineres av vanlige funksjoner. Abelske varianter er samtidig blant de mest studerte objektene innen algebraisk geometri og uunnværlige verktøy for mye forskning på andre emner innen algebraisk geometri og tallteori.
Lokalisering av en kategori: I matematikk består lokalisering av en kategori av å legge til en kategori inverse morfismer for en eller annen samling morfismer, og begrenser dem til å bli isomorfismer. Dette ligner formelt på prosessen med lokalisering av en ring; det gjør generelt gjenstander isomorfe som ikke var det før. I homotopiteori er det for eksempel mange eksempler på kartlegginger som er inverterbare opp til homotopi; og så store klasser av homotopi-like mellomrom. Beregning av brøker er et annet navn for å jobbe i en lokalisert kategori.
Abelsk variasjon: I matematikk, spesielt innen algebraisk geometri, kompleks analyse og algebraisk tallteori, er en abelsk variant en prosjektiv algebraisk variasjon som også er en algebraisk gruppe, dvs. har en gruppelov som kan defineres av vanlige funksjoner. Abelske varianter er samtidig blant de mest studerte objektene innen algebraisk geometri og uunnværlige verktøy for mye forskning på andre emner innen algebraisk geometri og tallteori.
Kompleks multiplikasjon av abelske varianter: I matematikk sies en abelsk variant A definert over et felt K å ha CM-type hvis den har en stor nok kommutativ subring i endomorfismen End ( A ). Terminologien her er fra kompleks multiplikasjonsteori, som ble utviklet for elliptiske kurver i det nittende århundre. En av de største prestasjonene innen algebraisk tallteori og algebraisk geometri fra det tjuende århundre var å finne de riktige formuleringene av den tilsvarende teorien for abelske varianter av dimensjon d > 1. Problemet er på et dypere abstraksjonsnivå, fordi det er mye vanskeligere å manipulere analytiske funksjoner av flere komplekse variabler.
Abelian von Neumann algebra: I funksjonell analyse er en abelisk von Neumann-algebra en von Neumann-algebra av operatører på et Hilbert-rom der alle elementene pendler.
Abelian von Neumann algebra: I funksjonell analyse er en abelisk von Neumann-algebra en von Neumann-algebra av operatører på et Hilbert-rom der alle elementene pendler.
Kommutatorundergruppe: I matematikk, nærmere bestemt i abstrakt algebra, er kommutatorundergruppen eller avledet undergruppe til en gruppe undergruppen generert av alle kommutatorene i gruppen.
Kommutatorundergruppe: I matematikk, nærmere bestemt i abstrakt algebra, er kommutatorundergruppen eller avledet undergruppe til en gruppe undergruppen generert av alle kommutatorene i gruppen.
Abelians: Abelianere var en kristen sekt som vokste opp på det 4. århundre på landsbygda nær Hippo Regius i Nord-Afrika under regjeringen til Arcadius. De bodde på kontinent som de bekreftet Abel. De ble pålagt å være gift, men ble forbudt å fullføre ekteskapet. Hvert par ble pålagt å adoptere to barn, en gutt og en jente. Da adoptivforeldrene deres døde, ville disse adopterte dannet et par og adoptert ytterligere to barn. Fordi ingen av Abels barn er nevnt i Skriften, antok abelerne at han ikke hadde noen. Dette synet ble påvirket av jødiske og manikanske-inspirerte gnostiske perspektiver på Abel som anerkjente at mens han var gift, forble han jomfru. Den eneste registreringen av sekten er i Augustine av Hippos De Haereticis ch. 87 , hvor han skriver at navnet på sekten sannsynligvis er av punisk opprinnelse. Ifølge Augustine ble sekten utryddet i 428 da de siste medlemmene konverterte til katolisismen.
Abelichnus: Abelichnus er en utdødd ichnogenus av dinosaurfotavtrykk fra Candeleros-formasjonen og Rio Limay-formasjonen. Typen ichnospecies, Abelichnus astigerrae , ble først oppdaget i Argentina og ble registrert som den største kjente dinosaur fotavtrykk noensinne oppdaget. Abelichnus vokste sannsynligvis til en størrelse på 12,5-13 meter lang.
Abelin: Abelin er et etternavn, og kan referere til: Jean-Pierre Abelin, fransk politiker Johann Philipp Abelin, tysk historiker Ernst Abelin, sveitsisk psykoanalytiker og grunnlegger av teorien om tidlig triangulering
Jean-Pierre Abelin: Jean-Pierre Abelin er en fransk politiker.
Abelin-reaksjon: Abelin-reaksjonen er en kvalitativ reaksjon for å demonstrere tilstedeværelsen av arsfenamin og neoarsfenamin i blod og urin.
Abeline's House: Abeline's House er et tidligere våningshus ved vannkanten ved Haurvig, like sør for Hvide Sande, Ringkøbing-Skjern kommune, på den danske vestkysten. Det ble omgjort til et lokalhistorisk museum for Holmsland Dunes på 1970-tallet og er nå en del av Ringkøbing – Skjern Museum.
Abilene, Kansas: Abilene er en by i og fylkeskommunen i Dickinson County, Kansas, USA. Fra og med folketellingen i 2010 var byens befolkning 6844. Dwight D. Eisenhower presidentbibliotek og museum ligger i Abilene. Abilene er også hjemmet til Greyhound Hall of Fame .
Abilene, Texas: Abilene er en by i Taylor og Jones-fylkene i Texas, USA. Dens befolkning var 117,063 ved folketellingen i 2010, noe som gjør den til den 27. mest folkerike byen i staten Texas. Det er hovedbyen i det statistiske området Abilene, som hadde en estimert befolkning på 123 420, fra og med 2019. Det er fylkesetet til Taylor County. Dyess Air Force Base ligger på vestsiden av byen.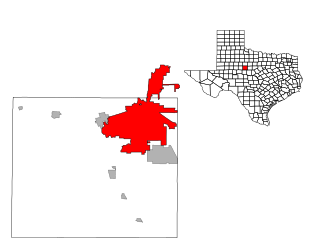
Abilene, Texas: Abilene er en by i Taylor og Jones-fylkene i Texas, USA. Dens befolkning var 117,063 ved folketellingen i 2010, noe som gjør den til den 27. mest folkerike byen i staten Texas. Det er hovedbyen i det statistiske området Abilene, som hadde en estimert befolkning på 123 420, fra og med 2019. Det er fylkesetet til Taylor County. Dyess Air Force Base ligger på vestsiden av byen.
Dyess Air Force Base: Dyess Air Force Base (AFB) er en amerikansk flyvåpenbase som ligger omtrent 11 km sørvest for Abilene, Texas.
Dyess Air Force Base: Dyess Air Force Base (AFB) er en amerikansk flyvåpenbase som ligger omtrent 11 km sørvest for Abilene, Texas.
Dyess Air Force Base: Dyess Air Force Base (AFB) er en amerikansk flyvåpenbase som ligger omtrent 11 km sørvest for Abilene, Texas.
Abelino Manuel Apeleo: Abelino Manuel Apeleo er en chilensk anglikansk biskop: tidligere hjelpebiskop i Araucanía, siden 2018 har han vært biskop i Temuco i den 40. og nyeste provinsen, Chile.
Abellio: Abellio var en gud tilbedt i Garonne-dalen i Gallia Aquitania, kjent hovedsakelig av en rekke påskrifter som ble oppdaget i Comminges, i Pyreneene. Han kan ha vært en gud av epletrær eller solen.
Chasselas: Chasselas eller Chasselas blanc er en druesort som vokser hovedsakelig i Sveits, Frankrike, Tyskland, Portugal, Ungarn, Romania, New Zealand, Kroatia og Chile. Chasselas er for det meste vinifisert til å være en full, tørr og fruktig hvitvin. Den er også egnet som en drue som dyrkes mye for dette formålet i Tyrkia og Ungarn.
Abellio: Abellio var en gud tilbedt i Garonne-dalen i Gallia Aquitania, kjent hovedsakelig av en rekke påskrifter som ble oppdaget i Comminges, i Pyreneene. Han kan ha vært en gud av epletrær eller solen.
Abeliophyllum: Abeliophyllum , miseonnamu , koreansk abeliophyllum , hvit forsythia eller koreansk abelialeaf , er en monotypisk slekt av blomstrende planter i olivenfamilien, Oleaceae. Den består av en art, Abeliophyllum distichum Nakai, endemisk mot Korea, hvor den er truet i naturen, og forekommer bare på syv steder. Det er relatert til Forsythia , men skiller seg ut fra å ha hvite, ikke gule blomster.
Abeliophyllum: Abeliophyllum , miseonnamu , koreansk abeliophyllum , hvit forsythia eller koreansk abelialeaf , er en monotypisk slekt av blomstrende planter i olivenfamilien, Oleaceae. Den består av en art, Abeliophyllum distichum Nakai, endemisk mot Korea, hvor den er truet i naturen, og forekommer bare på syv steder. Det er relatert til Forsythia , men skiller seg ut fra å ha hvite, ikke gule blomster.
Abelisauroidea: Abelisauroidea er en klade av theropod-dinosaurer i Ceratosauria. Noen kjente dinosaurer fra denne gruppen inkluderer abelisauridene Abelisaurus , Carnotaurus og Majungasaurus .
Abelisauroidea: Abelisauroidea er en klade av theropod-dinosaurer i Ceratosauria. Noen kjente dinosaurer fra denne gruppen inkluderer abelisauridene Abelisaurus , Carnotaurus og Majungasaurus .
Abelisauridae: Abelisauridae er en familie av ceratosaurian theropod dinosaurer. Abelisaurids trivdes i løpet av krittiden, på det gamle sørlige superkontinentet Gondwana, og i dag finnes deres fossile rester på de moderne kontinentene i Afrika og Sør-Amerika, så vel som på det indiske subkontinentet og øya Madagaskar. Rapporter basert på isolerte tenner viser forekomsten i Late Jurassic of Portugal, og den bekreftede eksistensen av europeiske abelisaurider kommer fra Late Cretaceous of France med Arcovenator . Abelisaurids dukker først opp i fossilregistreringen fra den tidlige midtre jura-perioden, og minst to slekter overlevde til slutten av Mesozoic-tiden for 66 millioner år siden.
Abelisauridae: Abelisauridae er en familie av ceratosaurian theropod dinosaurer. Abelisaurids trivdes i løpet av krittiden, på det gamle sørlige superkontinentet Gondwana, og i dag finnes deres fossile rester på de moderne kontinentene i Afrika og Sør-Amerika, så vel som på det indiske subkontinentet og øya Madagaskar. Rapporter basert på isolerte tenner viser forekomsten i Late Jurassic of Portugal, og den bekreftede eksistensen av europeiske abelisaurider kommer fra Late Cretaceous of France med Arcovenator . Abelisaurids dukker først opp i fossilregistreringen fra den tidlige midtre jura-perioden, og minst to slekter overlevde til slutten av Mesozoic-tiden for 66 millioner år siden.
Abelisauridae: Abelisauridae er en familie av ceratosaurian theropod dinosaurer. Abelisaurids trivdes i løpet av krittiden, på det gamle sørlige superkontinentet Gondwana, og i dag finnes deres fossile rester på de moderne kontinentene i Afrika og Sør-Amerika, så vel som på det indiske subkontinentet og øya Madagaskar. Rapporter basert på isolerte tenner viser forekomsten i Late Jurassic of Portugal, og den bekreftede eksistensen av europeiske abelisaurider kommer fra Late Cretaceous of France med Arcovenator . Abelisaurids dukker først opp i fossilregistreringen fra den tidlige midtre jura-perioden, og minst to slekter overlevde til slutten av Mesozoic-tiden for 66 millioner år siden.
Carnotaurini: Carnotaurini er en stamme av theropod-dinosaurfamilien Abelisauridae fra den sene krittperioden i Patagonia. Den inkluderer dinosaurene Carnotaurus sastrei ; typen arter, Aucasaurus garridoi , og Abelisaurus comahuensis . Denne gruppen ble først foreslått av paleontologene Rodolfo Coria, Luis Chiappe og Lowell Dingus i 2002, og ble definert som en klade som inneholdt " Carnotaurus sastrei , Aucasaurus garridoi , deres siste felles forfader, og alle dens etterkommere."
Abelisauroidea: Abelisauroidea er en klade av theropod-dinosaurer i Ceratosauria. Noen kjente dinosaurer fra denne gruppen inkluderer abelisauridene Abelisaurus , Carnotaurus og Majungasaurus .
Abelisauroidea: Abelisauroidea er en klade av theropod-dinosaurer i Ceratosauria. Noen kjente dinosaurer fra denne gruppen inkluderer abelisauridene Abelisaurus , Carnotaurus og Majungasaurus .
Abelisauroidea: Abelisauroidea er en klade av theropod-dinosaurer i Ceratosauria. Noen kjente dinosaurer fra denne gruppen inkluderer abelisauridene Abelisaurus , Carnotaurus og Majungasaurus .
Abelisaurus: Abelisaurus er en slekt av rovdyr abelisaurid theropod dinosaur levende i løpet av sen krittperiode (Campanian) i det som nå er Sør-Amerika. Det var et todelt rovdyr som sannsynligvis nådde omtrent 7,4 meter, selv om dette er usikkert da det bare er kjent fra en delvis hodeskalle.
Abelisaurus: Abelisaurus er en slekt av rovdyr abelisaurid theropod dinosaur levende i løpet av sen krittperiode (Campanian) i det som nå er Sør-Amerika. Det var et todelt rovdyr som sannsynligvis nådde omtrent 7,4 meter, selv om dette er usikkert da det bare er kjent fra en delvis hodeskalle.
Abelians: Abelianere var en kristen sekt som vokste opp på det 4. århundre på landsbygda nær Hippo Regius i Nord-Afrika under regjeringen til Arcadius. De bodde på kontinent som de bekreftet Abel. De ble pålagt å være gift, men ble forbudt å fullføre ekteskapet. Hvert par ble pålagt å adoptere to barn, en gutt og en jente. Da adoptivforeldrene deres døde, ville disse adopterte dannet et par og adoptert ytterligere to barn. Fordi ingen av Abels barn er nevnt i Skriften, antok abelerne at han ikke hadde noen. Dette synet ble påvirket av jødiske og manikanske-inspirerte gnostiske perspektiver på Abel som anerkjente at mens han var gift, forble han jomfru. Den eneste registreringen av sekten er i Augustine av Hippos De Haereticis ch. 87 , hvor han skriver at navnet på sekten sannsynligvis er av punisk opprinnelse. Ifølge Augustine ble sekten utryddet i 428 da de siste medlemmene konverterte til katolisismen.
Abelians: Abelianere var en kristen sekt som vokste opp på det 4. århundre på landsbygda nær Hippo Regius i Nord-Afrika under regjeringen til Arcadius. De bodde på kontinent som de bekreftet Abel. De ble pålagt å være gift, men ble forbudt å fullføre ekteskapet. Hvert par ble pålagt å adoptere to barn, en gutt og en jente. Da adoptivforeldrene deres døde, ville disse adopterte dannet et par og adoptert ytterligere to barn. Fordi ingen av Abels barn er nevnt i Skriften, antok abelerne at han ikke hadde noen. Dette synet ble påvirket av jødiske og manikanske-inspirerte gnostiske perspektiver på Abel som anerkjente at mens han var gift, forble han jomfru. Den eneste registreringen av sekten er i Augustine av Hippos De Haereticis ch. 87 , hvor han skriver at navnet på sekten sannsynligvis er av punisk opprinnelse. Ifølge Augustine ble sekten utryddet i 428 da de siste medlemmene konverterte til katolisismen.
Abelitz: Abelitz kan referere til: Abelitz (elv), en elv i Øst-Frisia, Tyskland Abelitz (Südbrookmerland), en landsby i Südbrookmerland, Øst-Frisia, Tyskland
Abelitz: Abelitz kan referere til: Abelitz (elv), en elv i Øst-Frisia, Tyskland Abelitz (Südbrookmerland), en landsby i Südbrookmerland, Øst-Frisia, Tyskland
Abelitz (elv): Abelitz er en elv i Niedersachsen, Tyskland, i Øst-Frisia. Den er omtrent 20 kilometer lang og flyter fra Marienhafe til munnen på Alte Greetsieler Sieltief . Denne typen elv som drenerer de lavtliggende polderne gjennom en slus i sjødypet er også lokalt kjent som en Tief og er ofte løpet av en gammel bekk mellom gjørme.
Abdul Qadir: Abd al-Qadir eller Abdulkadir er et mannlig muslimsk fornavn. Den er dannet av de arabiske ordene Abd , al- og Qadir . Navnet betyr "de kraftiges tjener", Al-Qādir er et av Guds navn i Koranen, noe som gir opphav til de muslimske teoforiske navnene.
Abdelkader El Brazi: Abdelkader El Brazi var en marokkansk fotballkeeper.
Abelkader Khamri: Abelkader Khamri var den algeriske ministeren for ungdom og sport i 1992-regjeringen til Belaid Abdessalam.
En bjelle: Abell kan referere til:
Adam Abell: Adam Abell var en skotsk friar ved Jedburgh Abbey. Han skrev en krønike på 1530-tallet som gir et innblikk i samtidens tanke og inneholder anekdoter som dukker opp i senere skrifter. Manuskriptet til Roit or Quheil of Tyme oppbevares på National Library of Scotland, MS 1746. Det ble donert av oberstløytnant WW Cunninghame of Caprington.
Alistair Abell: Alistair Abell er en kanadisk skuespiller, produsent og regissør som jobber i Vancouver, British Columbia, Canada. Han har uttalt flere roller i anime, særlig Colin MacLeod i Highlander: The Search for Vengeance og Lord Djibril i Gundam Seed Destiny . Han har også jobbet i videospill som Electronic Arts ' SSX 3 , og SSX On Tour .
Anthony Abell: Sir Anthony Foster Abell var en britisk kolonialtjenestemann som var guvernør i Sarawak og høykommissær i Brunei.
Abell, Baltimore: Abell er et nabolag som ligger i det nord-sentrale området av Baltimore, Maryland, USA. Det anses å være en del av Charles Village, Baltimore.
Ben Abell: Benjamin F. Abell var professor i meteorologi ved Institutt for jord- og atmosfærisk vitenskap ved Saint Louis University (SLU), hvor han var medlem av fakultetet fra 1962-2011. Han meldte seg også frivillig som eneste meteorolog for St. Louis, Missouri offentlige radiostasjon KWMU-FM siden stasjonen begynte å kringkaste i 1972 til begynnelsen av 2007. For å anerkjenne og bevare sine bidrag som et fremragende medlem av St. Louis radiosamfunn, var Abell en 2005–2006 induktiv til St. Louis Radio Hall of Fame.
Bud Abell: Harry Everett "Bud" Abell er en tidligere amerikansk fotball linebacker i American Football League for Kansas City Chiefs. Han spilte collegefotball ved University of Missouri.
Chris Abell: Christopher Abell var en britisk biologisk kjemiker. Han var professor i biologisk kjemi ved Institutt for kjemi ved University of Cambridge og Todd-Hamied Fellow fra Christ's College, Cambridge. Ved valget til Royal Society i 2016 beskrev samfunnet forskningen hans som å ha "endret ansiktet til narkotikafunn."
David Abell: David Abell kan referere til: Dave Abell, medlem av bandet Iced Earth David Abell (forretningsmann), britisk forretningsmann David Abell (komponist), dansk-tysk komponist og organist David Charles Abell, britisk amerikansk orkesterdirigent David H. Abell (c.1807–1872), politiker i New York
George Abell: George Abell kan referere til: George O. Abell (1927–1983), amerikansk astronom og pedagog George Abell (1904–1989), engelsk tjenestemann i Storbritannia og kolonialindisk tjeneste og cricketer
Joey Abell: Joey Abell er en amerikansk tungvektig profesjonell bokser. Han har møtt tidligere verdensmestere Tyson Fury, Chris Arreola, Tomasz Adamek, Kubrat Pulev, Fres Oquendo og Alfred Cole.
John Abell: John Abell var en skotsk countertenor, komponist og lutenist.
Joseph Abell: Joseph Abell var en sørafrikansk cricketer som spilte for Orange Free State i førsteklasses cricket fra 1921 til 1926.
Abell, Maryland: Abell er et ikke-innlemmet samfunn i det som kjent kalles "Seventh District" i St. Mary's County, Maryland, USA. Abell var en bryggeplate for mange fiskere og bønder på slutten av 1800-tallet til omtrent sent på 1950-tallet. Abell var kjent for sine mange store havner, og for tilgangen til dypt vann som gjorde det enkelt for store dampbåter å manøvrere. Mange av havnene er revet på grunn av stormer og orkaner. I dag bor fortsatt noen lokale fiskere i samme område der de ble oppdratt. Abell er også kjent for sine hundre år gamle hjem og utsikt over St. Clements Bay.
Peter Abell: Peter Abell er en britisk samfunnsforsker, for tiden professor emeritus ved London School of Economics hvor han har grunnlagt og ledet "Interdisciplinary Institute of Management". Han har undervist i mange år ved LSEs avdeling for ledelse, lederøkonomi og strategigruppe.
Richard Abell: Richard Abell var en britisk advokat og Whig-politiker som satt i Underhuset fra 1720 til 1727.
Robert Abell: Robert Abell ble født i ca 1605 i Stapenhill, Derbyshire, England. Han emigrerte til New England i 1630 som en del av den første bølgen av den store migrasjonen, og var blant de tidlige bosetterne i Massachusetts Bay Colony, og bosatte seg først i Weymouth, og deretter i Rehoboth, hvor han døde 20. juni 1663.
Roy Abell: Roy Beverley Abell var en engelsk midtlandsbasert kunstner. Han ble født i Small Heath, Birmingham og hadde en fremtredende karriere som maler og som kunstlærer. Han studerte ved Birmingham College of Art og ved Royal College of Art i London, og vendte tilbake til Birmingham for å undervise ved sitt tidligere college fra 1957 til 1982. Han ble sjef for malerskolen i 1974 og fungerte som medlem av Vesten. Midlands Arts - Fine Arts Panel.
Sam Abell: Sam Abell er en amerikansk fotograf kjent for sin hyppige publisering av fotografier i National Geographic .
William Abell: William Abell var en engelsk vinmester som ble mester i Vintners 'Company. Som politiker var han rådmann og senere lensmann i London. Han er assosiert med en kontrovers om måten og vilkårene som ble gitt monopol på vinmarkedet til medlemmer av Vintners 'Company.
Abell – Gleason House: Abell – Gleason House er et historisk hjem som ligger i Charlottesville, Virginia. Den ble bygget i 1859, og er en to-etasjers, tre-bay, gresk revival stil murstein bolig. Hver av buktene er definert av mursteinspilastre med doriske ordeninspirerte hovedsteder overfor stukkatur. Også på eiendommen er det en bidragsyter med fire rom.
Frank G. Abell: Franklin George Abell Jr. var en amerikansk fotograf aktiv i det vestlige USA på slutten av 1800- og begynnelsen av 1900-tallet.
Abell-Kilbourn House: Abell-Kilbourne House i Martinsburg, West Virginia er tilknyttet John N. Abell, en fremtredende Martinsburg-forretningsmann og Charles W. Kilbourn, en eier i Martinsburg-fabrikken. Den tidligere presidenten for den gamle nasjonale banken, Abell, utviklet området kjent som "Abells tilskudd" etter pensjonen i 1886. På den tiden bodde Abell på 506 West Burke Street.
Frank G. Abell: Franklin George Abell Jr. var en amerikansk fotograf aktiv i det vestlige USA på slutten av 1800- og begynnelsen av 1900-tallet.
Frank G. Abell: Franklin George Abell Jr. var en amerikansk fotograf aktiv i det vestlige USA på slutten av 1800- og begynnelsen av 1900-tallet.
En bjelle: Abell kan referere til:
Abell (etternavn): Abell er et engelsk etternavn, fra fornavnet Abel. Kjente personer med etternavnet inkluderer: Abraham Abell (1789–1851), irsk antikvar Sir Anthony Abell (1906–1994), britisk kolonialtjenestemann, guvernør i Sarawak Adam Abell (ca.1480 – c.1540), skotsk friar Alistair Abell, kanadisk stemmeskuespiller Arunah Shepherdson Abell (1806–1888), amerikansk forlegger Ben Abell, amerikansk meteorolog Bud Abell, amerikansk fotballspiller Chris Abell, britisk biologisk kjemiker David Abell (tvetydighet) , flere personer Derek F. Abell, amerikansk forretningsmann og pedagog Earl Abell (1892–1956), amerikansk fotballspiller Ferdinand Abell, amerikansk forretningsmann George Abell (tvetydighet) , flere personer Irvin Abell (1876–1949), amerikansk kirurg Joey Abell, amerikansk tungvektbokser John Abell (1653 – c.1724), skotsk musiker og komponist John Abell (cricketer) (1931–2004), engelsk cricketer Kjeld Abell (1901–1961), dansk dramatiker Louis Abell (1884–1962), amerikansk olympisk roer Peter Abell, britisk samfunnsforsker Richard Abell, britisk politiker Robert Abell (c.1605–1663), kolonial amerikansk innvandrer og pioner Roy Abell, engelsk cricketer og artist Sam Abell, amerikansk fotograf Stig Abell, britisk journalist Thomas Abel (c.1497–1540), engelsk prest og martyr Timothy Abell, engelsk cricketer Tom Abell, engelsk cricketer Walter Abell (1897–1956), amerikansk kunstlærer og teoretiker William Abell, (c.1584 – c.1655) Engelsk vintner Westcott Stile Abell, (1877-1961), britisk marinearkitekt
Hydra Cluster: Hydra-klyngen er en galaksehoper som inneholder 157 lyse galakser, som dukker opp i konstellasjonen Hydra. Klyngen strekker seg over ti millioner lysår og har en uvanlig høy andel mørk materie. Klyngen er en del av Hydra-Centaurus Supercluster som ligger 158 millioner lysår fra jorden. Klyngens største galakser er elliptiske galakser NGC 3309 og NGC 3311 og spiralgalaksen NGC 3312 som alle har en diameter på ca. 150 000 lysår. Til tross for et nesten sirkulært utseende på himmelen, er det bevis i galaksens hastigheter for en klumpete , tredimensjonal fordeling.
Abell 1146: Abell 1146 er en rik galaksehoper i konstellasjonen Crater. Dens rikdomsklasse er 4, og den ligger omtrent 2 milliarder lysår unna.
Abell 1185: Abell 1185 er en galaksehoper som ligger i konstellasjonen Ursa Major. Det er omtrent 400 millioner lysår unna jorden og strekker seg over en million lysår. Det er medlem av Leo Supercluster. En av de lyseste galaksene er NGC 3550.
Abell 12: Abell 12 er en planetarisk tåke som ligger i konstellasjonen Orion. Den er kjent som den "skjulte planetariske" tåken på grunn av forgrunnsstjernen Mu Orionis som gjør det vanskelig å observere.
Abell 1201 BCG: Abell 1201 BGC er en massiv elliptisk galaksesider som den lyseste klyngegalaksen til Abell 1201 galaksehoben. Ved en rød forskyvning på 0,169 ligger dette systemet rundt 2,7 milliarder lysår fra jorden, og forskjøvet omtrent 11 kiloparsek fra røntgenpunktet intrakluster gass. Med en elliptisitet på 0,32 ± 0,02 er stjernedistribusjonen langt fra sfærisk. I solenheter er den totale stjernelysstyrken 4 × 10 11 L ☉ i SDSS r-bånd, og 1,6 × 10 12 L ☉ i 2 MASS K- bånd. Halvstjernene kretser i en effektiv radius på 15 kpc, og deres sentrale hastighetsspredning er omtrent 285 km s -1 innen 5 kpcrising til 360 km s -1 på 20 kpc avstand.
Abell 13: Abell 13 er en planetarisk tåke av type 4 i konstellasjonen Orion. Den har en rødlig farge og er veldig svak.
Abell 133: Abell 133 er en galaksehoper i Abell-katalogen.
Leo Cluster: Leo-klyngen er en galaksehoper rundt 330 millioner lysår fjernt i konstellasjonen Leo, med minst 70 store galakser. Galaksen kjent som NGC 3842 er det lyseste medlemmet av denne klyngen. Sammen med Coma Cluster er det en av de to store klyngene som består av Coma Supercluster, som igjen er en del av CfA2 Great Wall, som er hundrevis av millioner lysår og er en av de største kjente strukturer i universet.
Abell 1413: Abell 1413 er en galaksehoper i Abell-katalogen. Abell-katalogen ble utgitt av George O. Abell i 1958 mens han jobbet med doktorgraden ved California Institute of Technology. Katalogen har to forskjellige undersøkelser. Den nordlige undersøkelsen ble gjort først av Abell i 1958 ved hjelp av AG Wilson. Den nordlige undersøkelsen har 2 712 klynger, og for at en klynge skal settes inn i katalogen, må den oppfylle fire kriterier. Det første kriteriet er rikdom, og Abell delte klyngene i 6 forskjellige rikdomsgrupper. Gruppe 0 var 30-49 galakser, Gruppe 1 var 50-79 galakser, Gruppe 2 var 80-129 galakser, Gruppe 3 var 130 til 199 galakser, Gruppe 4 var 200-299 galakser, og Gruppe 5 var mer enn 299 galakser. Det andre kriteriet var kompakthet. For å oppfylle dette kravet må en klynge ha 50 eller flere medlemmer i en telleradius for klyngens sentrum. Det tredje kriteriet er avstand. En klynge må ha en nominell rød forskyvning mellom .02 og .2, noe som betyr at en lavkonjunkturhastighet er mellom 6000 og 60.000 km / s. Det fjerde og siste kriteriet var galaktisk breddegrad. Områder rundt melkveien ble ekskludert fordi det var vanskelig å identifisere galaksehoper. Den sørlige undersøkelsen ble gjort i 1989 og la til 1 361 klynger ved å bruke samme kriterier som den nordlige undersøkelsen.
Coma Cluster: Coma-klyngen er en stor galakseklynge som inneholder over 1000 identifiserte galakser. Sammen med Leo Cluster er det en av de to store klyngene som består av Coma Supercluster. Det ligger i og tar navnet sitt fra konstellasjonen Coma Berenices.